Teoremele lui DeMorgan
DeMorgan a dezvoltat o serie de reguli importante in algebra liniara cu privire la complementul de grup. Prin complementul de grup ne referim la complementul unui grup de termeni, si nu doar complementul unei singure variabile.
Tineti minte de la capitolul legat de porti logice, ca inversand toate intrarile unei porti, inversam si functia logica esentiala a acesteia. O poarta SAU cu toate intrarile inversate (o poarta SAU-negativa) se comporta precum o poarta SI-negat. O poarta SI cu toate intrarile inversate (o poarta SI-negativa) se comporta precum o poarta SAU-negat. Teoremele lui DeMorgan exprima aceiasi echivalenta in sens invers: inversand iesirea unei porti, functia rezultata este aceiasi cu tipul opus de poarta cu intrarile inversate:
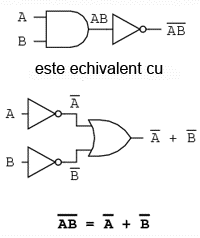
O bara deasupra termenului AB se comporta precum un simbol de grup. Acest lucru este total diferit fata de produsul AB inversat separat (A'B'). Cu alte cuvinte, (AB)' nu este egal cu A'B'. Acest lucru are un impact profund asupra modului de evaluare si de reducere a expresiilor booleene, dupa cum vom vedea.
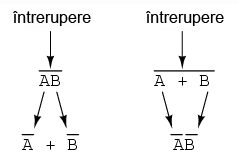
Teorema lui DeMorgan poate fi gandita ca si "intreruperea" complementului (bara orizontala). Atunci cand simbolul complementului este rupt in doua, operatia de sub el se modifica din adunare in inmultire si invers. Dupa aplicarea teoremei, fiecare variabila are propriul ei complement. Ca si exemplu:
Cand exista mai multe complemente deasupra aceleiasi expresii, nu putem intrerupe decat un complement pe rand. Cel mai usor este sa incepem cu cea mai lunga linie orizontala (cea de sus). Ca si exemplu, sa consideram expresia (A + (BC)')' redusa cu ajutorul teoremelor lui DeMorgan:
Urmand consideratiile exprimate mai sus, aplicam urmatorii pasi:

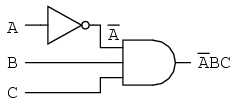
Ca si rezultat, circuitul original este redus la un circuit format dintr-o poarta SI cu trei intrari, unde intrarea A este inversata printr-o poarta NU:
Ca si contra-exemplu, nu intrerupeti niciodata mai mult de un complement la un singur pas:
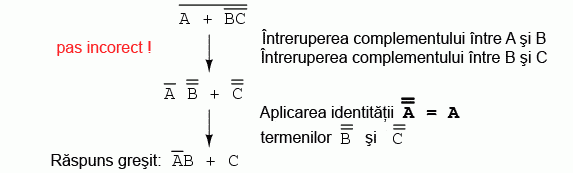
Pe cat de tentant pare, pe atat de incorect este sa scurtam pasii simplificarii prin intreruperea mai multor complemente deodata. Prin urmare, nu faceti niciodata acest lucru!
Putem simplifica expresia de mai sus si prin intreruperea complementului scurt in prima instanta, si apoi a complementului lung:
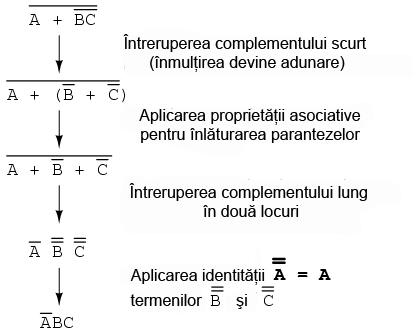
Desigur, rezultatul final este acelasi si in acest caz. Pasii necesari pentru simplificare sunt insa mai numerosi fata de exemplul precedent (intreruperea complementului lung la primul pas). La pasul al treilea, in exemplul de mai sus, intreruperea complementului lung se realizeaza in doua locuri simultan. Aceasta operatie matematica este permisa, si nu este identica cu intreruperea a doua complemente deodata! Interdictia intreruperii mai multor complemente deodata nu interzice intreruperea complementului in mai multe locuri.
Poate va intrebati de ce am folosit paranteze in jurul sub-expresiei B' + C', din moment ce oricum le-am indepartat la pasul urmator. Am facut acest lucru pentru a sublinia un aspect important dar neglijat al teoremei lui DeMorgan. Din moment ce o linie orizontala lunga functioneaza ca si simbol de grup, variabilele incluse sub aceasta trebuie sa ramana grupate. In caz contrar, ordinea operatiilor se pierde. In exemplul anterior, nu conteaza daca am fi pus sau nu aceste paranteze, dar in alte cazuri s-ar putea sa conteze. Sa luam un alt exemplu, mentinand parantezele:
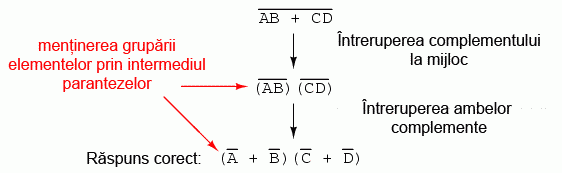
In cazul in care nu mentinem parantezele, riscam sa obtinem un raspuns gresit:
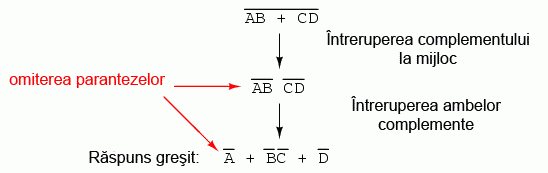
Dupa cum se poate observa, mentinerea gruparii realizate implicit prin liniile de complementare este cruciala pentru obtinerea raspunsului corect.
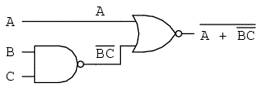
Sa aplicam acum principiile teoremelor lui DeMorgan pentru simplificarea unui circuit cu porti logice:
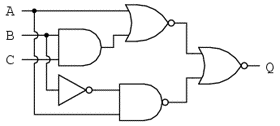
Ca de obicei, primul pas al simplificarii circuitului consta in gasirea expresiei booleene echivalente. Putem face acest lucru prin notarea sub-expresiilor la iesirea fiecarei porti, pe masura ce intrarile ne sunt cunoscute:
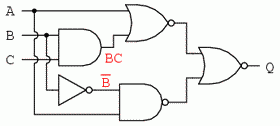
Apoi, notam iesirea primei porti SAU-negat si iesirea portii SI-negat. Atunci cand aveam de-a face cu porti inversate pe iesire, este mai usor sa scriem prima data expresia fara inversarea finala. Observati si de pe figura faptul ca sageata indica iesirea portii chiar inaintea inversarii (cerculetul de la iesire). Expresia finala, dupa inversare, este complementul expresiei precedente. Astfel, ne putem asigura ca nu uitam introducerea complementului in cadrul expresiei:
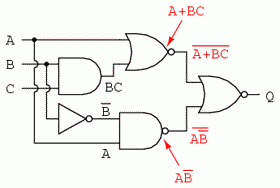
Si, in sfarsit, ultimul pas consta in scrierea expresiei pentru poarta SAU-negat finala:
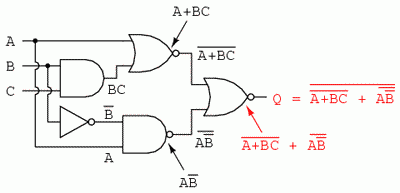
Trecem apoi la reducerea acestei expresii folosind identitatile, proprietatile, regulile si teoremele (lui DeMorgan) algebrei booleene:
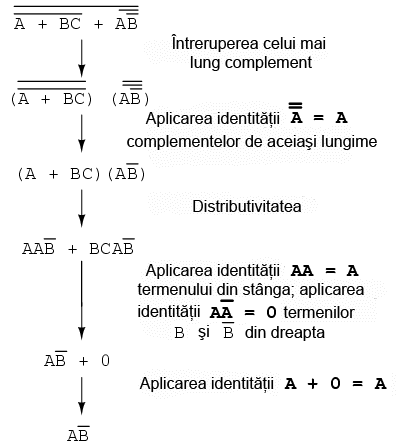
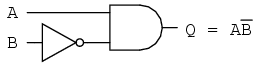
Circuitul echivalent al expresiei mult simplificate:
|
Politica de confidentialitate |
| Copyright ©
2026 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |