Criterii de optimalitate in teoria deciziilor
In acest moment se cunosc foarte multe tehnici prin care se pot realiza rezolvarea unei probleme de optimizare (cu sau fara restrictii, dinamica sau de tip minmax). Problema este stabilirea efectiva a functiei de eficienta in diferite situatii: exista unul sau mai multi decidenti, exista posibilitatea cooperarii corealizarii sau interesele decidentilor sunt diferite, se pot cuantifica corect multimea de decizie pentru fiecare decident, se pot stabili parametrii corectori, se pot evalua corect castigurile informationale etc.
Criteriile de optimalitate in teoria deciziilor sunt impartite in trei categorii, in functie de conditiile in care este creat modelul de lucru .
1. Conditii deterministe
Se considera a fi acela in care o actiune conduce la un singur rezultat. Din punct de vedere matematic aceasta inseamna ca se lucreaza doar cu functii univoce adica acele functii care asociaza unei valori din domeniu o singura valoare din codomeniu. Practic acest caz se incadreaza in conditiile obisnuite ale teoriei optimizarii, subiect dezvoltat in capitolul urmator (evident vor fi prezentate doar rezultatele centrale).
2. Conditii nedeterministe
Presupunem
ca avem un proces decizional cu cel putin doi decidenti pentru
care notam cu f functia de
eficienta. Din motive legate de comoditatea calculelor vom presupune
ca exista doar doi decidenti pentru care vom nota cu ![]()
![]() multimile de
decizie si cu
multimile de
decizie si cu ![]() care in mod uzual se
poate scrie sub forma
care in mod uzual se
poate scrie sub forma ![]() si care se
numeste matricea platilor.
si care se
numeste matricea platilor.
Din punct de vedere economic semnificatia multimilor X si Y este diversa. Cazul cel mai comod este acela in care avem un proiect investitional de cost dat si exista mai multe posibilitati de realizare al acestuia; aceste posibilitati fiind cuantificate prin elementele x1, x2, ., xm ale multimii X [37].
Pentru a nu risca situatiile in care angajamentele ocazionate de realizarea proiectului sa nu fie acoperite, este necesar ca incasarile sau profiturile obtinute sa fie asigurate. Exista in total n posibilitati de asigurare, practic acest lucru fiind reflectat de elementele multimii Y.
Din considerente practice ultima varianta, desemnata prin elementele multimii Y semnifica faptul ca profitul nu este asigurat. In acest caz f reprezinta functia de profit, iar Bij reprezinta profitul adus prin realizarea proiectului in varianta xi si in baza asigurarii yj. Din motive de comoditate ale notatiilor, perechea (xi, yj) se noteaza simplu (i, j).
Conditiile
nedeterministe se exprima prin faptul ca primul decident nu are
informatii suficiente asupra multimii de decizie Y ale celui de-al doilea decident. Aceasta inseamna ca nu
se poate formula corect problema ![]() prin urmare trebuie
cautate criteriile speciale de comportament strategic.
prin urmare trebuie
cautate criteriile speciale de comportament strategic.
2.1. Criteriul optimist (Hurcwitz)
Acest criteriu presupune alegerea acelei perechi de strategii (xi0, yj0), practic a perechii (i0, j0) pentru care se realizeaza egalitatea urmatoare:
![]()
In aceasta situatie p reprezinta gradul de optimism al primului decident legat de alegerea celei mai avantajoase situatii.
Observatia
Utilizarea acestui criteriu este extrem de
comoda deoarece presupune un calcul imediat pornind de la matricea
profiturilor ![]() dar nu conduce la
rezultate concludente intru-cat alegerea parametrului p este in general subiectiva.
dar nu conduce la
rezultate concludente intru-cat alegerea parametrului p este in general subiectiva.
Observatia
1.3. Marimea
p are semnificatia unei ponderi
si din acest motiv se impune conditia ![]() .
.
2.2. Criteriul pesimist (Wald)
Potrivit
acestui criteriu strategia optima (i0,j0)
este aleasa asa incat valoarea optima obtinuta este
aceea pentru care se realizeaza egalitatea ![]() .
.
Din
punct de vedere economic profitul optim ![]() in raport cu acest criteriu semnifica cel mai mare
profit pe care il poate realiza primul decident indiferent de comportamentul
strategic al celui de-al doilea.
in raport cu acest criteriu semnifica cel mai mare
profit pe care il poate realiza primul decident indiferent de comportamentul
strategic al celui de-al doilea.
In
cazul exemplului legat de proiectul investitional ![]() reprezinta
profitul cel mai mare pe care il poate obtine investitorul indiferent de
varianta de asigurare adoptata de catre celalalt decident.
reprezinta
profitul cel mai mare pe care il poate obtine investitorul indiferent de
varianta de asigurare adoptata de catre celalalt decident.
Observatia
1.4.
Acest criteriu a fost preluat din teoria jocurilor, iar marimea ![]() reprezinta
castigul maxim garantat, practic:
reprezinta
castigul maxim garantat, practic:
![]()
2.3. Criteriul Neumann
Potrivit
acestui criteriu strategia optima este acea pereche (i0,j0) pentru care profitul optim este dat
de egalitatea urmatoare: ![]() .
.
Din
punct de vedere economic profitul ![]() reprezinta pierderea maxima pe care o poate realiza
decidentul al doilea, indiferent de comportamentul strategic al primului
decident.
reprezinta pierderea maxima pe care o poate realiza
decidentul al doilea, indiferent de comportamentul strategic al primului
decident.
Observatia 1.5. Se poate arata relativ usor urmatoarea inegalitate:
![]() .
.
2.4. Criteriul (principiul) stabilitatii
Este
un criteriu introdus de Neumann in baza caruia perechea (i0,j0) trebuie
cautata pornind de la egalitatea urmatore: ![]() .
.
O astfel de pereche optima se numeste punct de echilibru si se caracterizeaza in general printr-un comportament strategic prudent.
Determinarea perechii (i0,j0) pentru care se realizeaza egalitatea precedenta este o problema, in general, dificila si se rezolva printr-o tehnica speciala de optimizare, optimizare minmax.
A. Criteriul stabilitatii in strategii simple
Practic suntem condusi la rezolvarea problemei de optimizare:
(P)
![]()
care, in contextul analizat devine:
![]()
Se
poate arata ca solutia ![]() a problemei (P) verifica conditiile:
a problemei (P) verifica conditiile:
![]() ,
,
ceea ce din punct de vedere a deciziilor inseamna ca orice abatere a decidentilor de la alegerea strategiei echilibru va conduce la micsorarea castigurilor acestora.
Rezolvarea problemei (P) este in general dificila. De asemenea trebuie precizat ca nu totdeauna aceasta problema are solutii. Atunci cand existenta solutiilor este asigurata, metodele uzuale folosite pentru determinarea punctelor echilibru sunt urmatoarele: metoda multiplicatorilor lui Lagrange, metoda penalizarii, metoda gradientului etc.
B. Criteriul stabilitatii in strategii mixte
Se porneste de la acceptiunea ca in general o matrice a castigurilor (profiturilor) nu contine puncte de echilibru. Altfel spus egalitatea
![]() ,
,
nu are intotdeauna solutie. In consecinta functia de eficienta f a fost modificata corespunzator, multimile de strategii au fost si ele modificate astfel incat in noile conditii sa se poata determina intotdeauna punctele de echilibru.
Asociem multimilor de strategii X, Y asa numitele multimi de strategii mixte P, Q unde P reprezinta multimea tuturor repartitiilor de probabilitate
![]() ,
,
iar Q reprezinta multimea tuturor repartitiilor de probabilitate
![]()
Semnificatia componentelor pi si qj a strategiilor mixte p, respectiv q este urmatoarea:
.
componenta pi a strategiei
mixte P semnifica faptul ca
primul decident adopta strategia xi
cu probabilitatea pi, ![]() .
.
.
componenta qj a strategiei
mixte Q semnifica faptul ca
cel de-al doilea decident adopta strategia yj cu probabilitatea qj,
![]() .
.
Se
introduce o noua functie de eficienta ![]() , definita prin egalitatea:
, definita prin egalitatea:
![]()
Aceasta functie de eficienta semnifica profitul mediu obtinut de cei doi decidenti (deoarece este de fapt valoarea medie a unei variabile aleatoare).
Pentru noua functie de eficienta F se poate arata ca totdeauna exista puncte de echilibru in strategii mixte.
Teorema 1.1. [15] Au loc urmatoarele rezultate:
a) exista totdeauna un
punct de echilibru ![]() unde:
unde:
![]()
![]()
componentele acestor strategii fiind date de egalitatile urmatoare:


unde: ![]() sunt solutiile
optime ale urmatorului cuplu dual de probleme de optimizare liniara:
sunt solutiile
optime ale urmatorului cuplu dual de probleme de optimizare liniara:

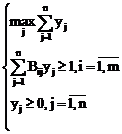
Valoarea functiei de eficienta pentru punctul echilibru gasit este urmatoarea:
 .
.
2.5. Criteriul regretului minim (Savage)
Are la baza analiza efectelor alegerii unei variante proaste in raport cu o varianta buna. Potrivit acestui criteriu perechea optima cautata (i0,j0) este aceea pentru care se realizeaza egalitatea urmatoare:
![]()
Semnificatia marimilor care intervin in aceasta egalitate sunt urmatoarele:
1)
Daca al doilea decident adopta strategia j, atunci profilul primului decident este ![]() ;
;
2)
![]() reprezinta
pierderea maxima a primului decident datorata alegerii strategiei j de catre al doilea decident;
reprezinta
pierderea maxima a primului decident datorata alegerii strategiei j de catre al doilea decident;
3)
![]() reprezinta
maximul tuturor pierderilor realizate de catre primul decident;
reprezinta
maximul tuturor pierderilor realizate de catre primul decident;
4)
![]() reprezinta
pierderea minima realizata de catre primul decident.
reprezinta
pierderea minima realizata de catre primul decident.
Altfel spus, daca presupunem ca al doilea decident adopta strategia j, atunci maximul pierderii de profit al primului decident este de 2). Analizand insa toate variantele, pierderea maxima este data de 3). In consecinta primul decident va adopta aceea decizie i0 pentru care se realizeaza minimul dat de 4).
3. Conditii de incertitudine
Corespunde situatiei in care y este o variabila aleatoare pentru care se cunoaste exact functia de repartitie sau functia de repartitie poate fi bine aproximata.
Asociem
multimii ![]() o repartitie de
probabilitati
o repartitie de
probabilitati ![]() ,
, ![]()
![]() .
.
Semnificatia marimilor p1, p2, ., pn este legata de ponderile alocate elementelor multimii de decizie pentru primul decident.
3.1. Criteriul verosimilitatii maxime
Potrivit acestui criteriu decizia optima consta in alegerea acelei perechi (i0,j0) pentru care se realizeaza urmatoarea egalitate:
![]()
Astfel spus, strategia optima i0 a primului decident corespunde alegerii ponderii maxime, iar strategia optima j0 a celui de al doilea decident corespunde situatiei de maximizare a profitului.
3.2. Criteriul profitului mediu (Bayes)
Acest criteriu de optim are la baza ideea utilizarii notiunii de valoare medie. Potrivit acestui criteriu se va alege varianta optima j0 pentru care se maximizeaza profitul mediu.
Vom nota cu Pj profitul mediu pentru varianta j,
![]()
Solutia
optima cautata este j0
pentru care ![]() .
.
In
situatia in care ponderile nu sunt cunoscute, acest criteriu permite
determinarea optimala a lor din conditiile ![]() . Aceste conditii impreuna cu conditia
. Aceste conditii impreuna cu conditia ![]() conduce la un sistem
liniar de n ecuatii cu n necunoscute.
conduce la un sistem
liniar de n ecuatii cu n necunoscute.
3.3. Criterii entropice
Sunt cunoscute trei criterii distincte:
criteriul informatiei maxime simple ;
criteriul informatiei maxime ponderate;
criteriul informatiei maxime si a valorii medii (in sensul de suma dintre entropie si valoarea medie).
A. Criteriul informatiei maxime simple
Practic
se pune problema determinarii acelei repartitii de
probabilitati ![]() (ponderile
profiturilor) pentru care se maximizeaza entropia. In mod obisnuit
restrictiile problemei sunt legate de cunoasterea in prealabil a unor
indicatori statici, in mod uzual sau media si abaterea medie
patratica.
(ponderile
profiturilor) pentru care se maximizeaza entropia. In mod obisnuit
restrictiile problemei sunt legate de cunoasterea in prealabil a unor
indicatori statici, in mod uzual sau media si abaterea medie
patratica.
In situatia in care se cunosc valorile medii:
![]() (1.1)
(1.1)
suntem condusi la rezolvarea urmatoarei probleme de optimizare liniara:
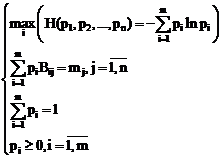
In mod obisnuit aceasta problema se rezolva utilizand metoda multiplicatorului lui Lagrange. Solutia acestei probleme este urmatoarea:
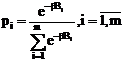
unde: ![]() ; iar b reprezinta solutia
unica a urmatoarei ecuatii:
; iar b reprezinta solutia
unica a urmatoarei ecuatii:
![]() (1.2)
(1.2)
Observatia 1.6. Membrul drept al egalitatii (2.2) este de fapt un profit mediu ponderat, ceea ce inseamna ca valoarea medie mj are o semnificatie economica bine precizata.
B. Criteriul informatiei maxime ponderate
In aceasta situatie functia de eficienta se considera a fi entropia lui Guiasu:
![]()
Ne intereseaza acea repartitie de probabilitate care maximizeaza entropia, deci suntem condusi la rezolvarea urmatoarei probleme:

Solutia
acestei probleme se poate determina utilizand metoda multiplicatorului lui
Lagrange, fie utilizand un artificiu si cateva rezultate importante din
calculul diferential. In final se obtine: ![]() ; unde a reprezinta solutia
unica a ecuatiei:
; unde a reprezinta solutia
unica a ecuatiei:
![]()
Observatia
1.7. Din
punct de vedere economic conditia ![]() este cunoscuta
sub denumirea de conditie exclusivista, fiind de fapt echivalentul
matematic al conditiei de independenta probabilista.
este cunoscuta
sub denumirea de conditie exclusivista, fiind de fapt echivalentul
matematic al conditiei de independenta probabilista.
C. Criteriul maximizarii informatiei si a valorii medii
Practic suntem condusi la rezolvarea urmatoarei probleme:
![]()
Tinand
seama de conditia de exclusivitate ![]() si de
conditia de nenegativitate
si de
conditia de nenegativitate ![]() dupa aplicarea
metodei multiplicatorului lui Lagrange obtinem imediat solutia
cautata:
dupa aplicarea
metodei multiplicatorului lui Lagrange obtinem imediat solutia
cautata:
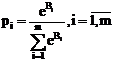
Observatia 1.8. In cazul in care ne situam in varianta maximizarii unei variabile aleatoare continue pentru care se cunoaste valoarea medie m si abaterea medie patratica s, aplicand principiul informatiei maxime simple, rezulta dupa un calcul relativ comod ca distributia optima care maximizeaza informatia este de tip normal cu parametrii m si s adica de tipul N(m, s
4.4.Probleme rezolvate
Aplicatia 1. Sa se determine solutia Wald, Neumann si Harcwitz pentru o matrice a platilor date de egalitatea:

Rezolvare
a) Solutia Wald (pesimista)
consta in determinarea acelei perechi i0 si j0
pentru care ![]() . Vom fixa pe rand indicele "i" si vom calcula pentru
fiecare caz
. Vom fixa pe rand indicele "i" si vom calcula pentru
fiecare caz ![]() , dupa care vom calcula indicele "i0" care
realizeaza maximul acestor minime.
, dupa care vom calcula indicele "i0" care
realizeaza maximul acestor minime.

Solutia se determina imediat daca se calculeaza pentru fiecare linie un numar si se selecteaza cel mai mare din aceste numere.
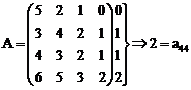 .
.
b) Solutia Neumann consta in determinarea acelei perechi (i0,j0) pentru care avem
![]() .
.
Fixam pe rand pe "j" si calculam maximele, dupa care vom determina cel mai mic dintre aceste maxime.

Se
constata ca are loc egalitatea urmatoare: ![]() . Prin urmare perechea
. Prin urmare perechea ![]() este punct de
echilibru.
este punct de
echilibru.
c) Solutia optimista (Harcwitz)
Se presupune ca gradul de optimism cu privire la alegerea celei mai avantajoase solutii este p = 0,8. Vom determina perechea (i0, j0) pentru care are loc egalitatea:
![]()

Aplicatia 2 Sa se gaseasca punctul echilibru in strategii mixte in situatia in care matricea platilor este:
![]()
Rezolvare:
Strategia
optima ![]() , unde:
, unde:
![]()
se poate determina ca solutie a unui cuplu de probleme de optimizare liniara duala.
Matricea linie este de forma urmatoare: j = (1 1).
In cazul particular in care matricea are 2 linii si 2 coloane solutia este:
![]()
unde: . A* reprezinta reciproca matricei A;
. AT reprezinta transpusa matricei A.
Reciproca A* se calculeaza din transpusa AT inlocuind fiecare element al matricei cu complementul sau algebric.
Transpusa este 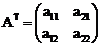 , iar inversa este
, iar inversa este ![]() .
.
Calculam:
![]()
si
![]() .
.
Deci ![]() ,
,
unde
![]() si
si ![]()
![]() ,
,
unde
![]() si
si ![]() .
.
Aplicatia
3. Se da
matricea de forma urmatoare: ![]() .
.
a) Sa se verifice daca exista punct de echilibru in strategii simple;
b) Sa se gaseasca punctul de echilibru in strategii mixte.
Rezolvare:
a) In
strategii simple exista punct de echilibru daca are loc relatia
urmatoare: ![]() .
.

Se observa
ca ![]() deci nu exista
punct de echilibru.
deci nu exista
punct de echilibru.
b) In
strategiile mixte trebuie determinata perechea ![]() pentru care au loc
relatiile urmatoare:
pentru care au loc
relatiile urmatoare:
![]() cu
cu ![]() , respectiv
, respectiv ![]() cu
cu ![]() .
.

|
Politica de confidentialitate |
| Copyright ©
2026 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |