
Notiuni de statistica matematica aplicate in educatia fizica si sport
Statistica, ca ramura a matematicii este folosita in cele mai variate stiinte pentru prelucrarea datelor inregistrate. Notiunile de baza ale statisticii sunt abstractii foarte cuprinzatoare prin care reusim sa ne apropiem de fenomenul studiat si sa-i intelegem semnificatia.
Valoarea indicelui statistic folosit depinde in mod direct de valoarea inregistrarilor obtinute prin diferitele metode de cercetare (experiment, ancheta, observatie etc.).
Desi aplicarea metodelor statistice presupune aplicarea in prealabil a altor metode prin care se obtine sirul de date ce urmeaza a fi relucrate, statistica nu se reduce numai la prelucrare, ci prin intermediul ei posibilitatea de cunoastere a fenomenului se largeste, judecata reusind sa desprinda din inregistrarile brute si izolate legile dupa care se desfasoara fenomenele, sa sesizeze unitatea dintr-o larga diversitate.
Exista doua categorii de legi: legi dinamice (actioneaza in cazul fenomenelor individuale luate ca atare si legi statistice care actioneaza in cazul fenomenelor de masa (apar ca o rezultanta medie a numeroaselor actiuni individuale ale ansamblului de fenomene).
Legea statistica se deosebeste de legea dinamica prin aceea ca nu exclude posibilitatea aparitiei fenomenelor aleatorii, ca nu poate fi confirmata sau infirmata de un caz individual si nici nu poate sa ne conduca la previziuni pentru fiecare caz individual (luat ca atare). Previziunea este valabila in medie pentru un anumit numar de cazuri din categoria fenomenelor studiate si probabila fiecarui caz.
Probabilitatea este cu atat mai mare cu cat numarul fenomenelor studiate (esantionul) este mai mare. Frecventa empirica tinde catre probabilitatea teoretica p in cazul esantioanelor largi, dar diferenta p -f nu se micsoreaza neincetat prin prin cresterea numarului cazurilor, ci oscileaza aleatoriu in jurul lui 0 (zero).
Statistica isi exprima rezultatele in date cifrice si foloseste ca procedeu de baza numaratoarea si gruparea.
V. Sahleanu distinge o serie de probleme a caror rezolvare este ajutata de statistica, intre acestea sunt:
- Probleme de ordonare - urmaresc desprinderea a ceea ce este mai frecvent sau mai important;
- Probleme de structura - cunoasterea structurii unei colectivitati, acestea se realizeaza in special cu ajutorul poligoanelor de frecventii;
- Probleme de caracterizare cantitativa a particularitatilor colectivitatii - prin medie, modul, mediana, abatere medie, patratica, etc.;
- Probleme de variabilitate - pentru caracterizarea variabilitatii este necesara stabilirea dispersiei;
- Probleme ale interpretarii datelor numerice unde se apreciaza exactitatea si precizia rezultatelor;
- Probleme de variatie legata. Se poate stabili si masura legatura intre diverse fenomene cu ajutorul coeficientilor de corelatie.
Aceste probleme ne ajuta la realizarea unei evidente a materialului studiat (statistica descriptiva), la desprinderea relatiilor intre diverse fenomene sau intre diferitele laturi ale aceluiasi fenomen (statistica analitica) si in inductia stiintifica.
Cercetarile stiintifice nu se fac de obicei epuizand cazurile, ci pe un anumit esantion. Se pune problema in ce masura datele obtinute asupra esantionului sunt valabile colectivitatii generale. Metoda statistica poate preciza numeric, prin valoarea unei probabilitati, limitele increderii intr-un rezultat numeric de observatie sau experiment (statistica inductiva).
Fenomenele studiate (izolat sau in raporturile dintre ele) de catre diferite discipline stiintifice se impart, din punct de vedere al metodei intrebuintate in studierea lor, in doua categorii:
- fenomene tipice;
- fenomene colective.
Fenomenele tipice sunt acele fenomene care, in conditii identice sau asemanatoare, se prezinta sub aceeasi forma unica (asa se prezinta majoritatea fenonenelor din lumea anorganica).
Fenomenele colective sunt acele fenomene care nu se pot reproduce aproape niciodata in mod identic. Dintre acestea fac parte si fenomenele biologice si cele sociale, deci si fenomenele care privesc activitatea de educatie fizica si sport.
Aplicarea metodelor statisticii matematice in prelucrarea si analizarea unor fenomene intalnite in activitatea de educatie fizica si sport este justificata prin caracterul probabilistic al acestor fenomene, care intra in grupa fenomenelor colective. Studierea cu ajutorul statisticii matematice a caracteristicilor diferitelor fenomene de educatie fizica si sport permite:
- descrierea mai exacta a acestor fenomene;
- delimitarea mai riguroasa a problemelor, prin introducerea unei ordini precise si, deci, prin realizarea unui tablou general unitar;
- prevederea unor fenomene care vor putea avea loc daca acestea se repeta in conditii asemanatoare sau identice celor care au fost studiate mai inainte;
- analizarea unor factori cauzali, in afara celor perturbatori.
Studiul diferitelor fenomene colective nu se poate face decat pe baza unui numar relativ mare de cazuri, pentru a se putea separa ceea ce este tipic de ceea ce este intamplator si a se distinge elementul trecator de cel permanent.
Cercetarea statistica a fenomenelor colective se desfasoara in trei etape:
1. observarea statistica a caracteristicilor colectivitattii studiate (alegerea unitatilor care urmeaza a fi cercetare; obtinerea materialului statistic prin inregistrarea intr-o forma unitara a caracteristicilor care ne intereseaza);
2. centralizarea, ordonarea si prelucrarea datelor culese in cursul observarii, calculul indicatorilor sintetici, care caracterizeaza colectivitatea cercetata, prezentarea graficelor care usureaza analiza datelor culese;
3. aprecierea si analiza indicatorilor sintetici, care caracterizeaza colectivitatea fenomenelor studiate.
In cercetarea statistica a fenomenelor din domeniul educatiei fizice, pentru a se trage concluzii care sa poata fi extinse asupra intregii colectivitati de fenomene studiate, este necesara alegerea unui esantion reprezentativ (numeric).
Esantionul este un grup de subiecti selectat pentru efectuarea unui experiment asupra lui. Cum se efectueaza esantioanele?
1. Selectia aleatoare* se realizeaza astfel: identificare (exista o tabela Fischer de numere aleatorii, de asemenea pot fi utilizate si programele pe computer), dupa care, folosind diferite criterii, sunt selectati subiectii. Acestia formeaza un esantion reprezentativ pentru intreaga populatie din care face parte, adica observatiile relevate de acest grup pot fi generalizate la intreaga populatie.
2. Esantionarea aleatoare stratificata. In acest caz populatia este impartita dupa o anumita caracteristica inainte de selectia aleatoare.
3. Esantionarea sistematica poate fi realizata prin telefon (fiecare al 50-lea abonat).
4. Desemnarea aleatoare se refera la posibilitatea desemnarii de grupe in interiorul esantionului.
Prezentarea datelor sub forma de tabele
Datele primare odata grupate sunt centralizate in tabele care usureaza cuprinderea materialului si desprinderea aspectelor esentiale. Modul de intocmire a tabelelor depinde de obiectivele cercetarii, de aspectele care urmeaza a fi scoase in evidenta.
Adeseori se intocmesc tabele comparative, iar grupele studiate pot sa aiba efective inegale. In acest caz, frecventele stabilite trebuie exprimate in procente (frecvente relative).
N = efectiv total se ia la 100%
si se aplica regula de trei simpla. De exemplu:
Daca 24 . 100%
atunci 6 .. x
x = ![]() =
= ![]() = 25%
= 25%
Datorita accesibilitatii sale, exprimarea procentuala este preferata in multe cercetari. In unele cazuri recurgem la calcularea procentului sau indicelui de exactitate
E = indice de exactitate
si se calculeaza dupa formula:
E =![]() . 100
. 100
in care:
Rc reprezinta numarul de raspunsuri corecte (incercari reusite), iar
R max reprezinta numarul maxim de raspunsuri (puncte, incercari) posibil de realizat
Exemplu: avem trei clase de elevi cu efective dupa cum urmeaza:
Tabelul 26.1 Punctajul pentru raspunsurile corecte ale elevilor cuprinsi in experiment
|
Clasa |
nr. elevi |
nr. maxim de puncte |
raspunsuri corecte |
|
de experienta A |
37 |
444 |
364 |
|
B |
29 |
348 |
285 |
|
de control C |
41 |
492 |
315 |
Fiecare elev are de efectuat 6 aruncari la cos din care poate realiza 12 puncte.
Se calculeaza procentul (indicele de exactitate) astfel:
EA = ![]() x 100 = 81,98 82%
x 100 = 81,98 82%
EB = ![]() x 100 = 81,89 82%
x 100 = 81,89 82%
EC = ![]() x 100 = 64,02 64%
x 100 = 64,02 64%
Se considera ca actiunea (priceperea) este insusita cand intruneste 75% exactitate.
Tabelele trebuie astfel intocmite incat sa poata fi citite cu usurinta. Pentru a nu fi prea incarcate, uneori reducem numarul categoriilor, contopind intervale invecinate. Exemplu: notele obtinute de studenti:
foarte bune bune mediocre slabe
10 - 9 8 - 7 6 - 5 4 –3
Tabelul 26.2
Notele obtinute de subiecti
Tabelul se prezinta astfel:
|
Grupa |
numar |
Rezultate |
|||
|
|
stud. |
F.b. |
B |
M |
S |
|
exp. |
32 |
5 |
7 |
18 |
2 |
|
Control. |
20 |
2 |
4 |
10 |
3 |
Precizarea numarului de subiecti care compun grupele studiate este obligatorie. Cand N este mic nu se recurge la exprimare procentuala (deoarece ne poate induce in eroare).
Un tabel poate fi mai complet daca prezinta datele, atat in cifre absolute (N) cat si in procente (%).
In orice tabel distingem doua elemente: coloana (pe verticala) si linia sau randul (pe orizontala). Este bine ca orice tabel sa aiba un numar si un titlu, notate deasupra, care sa redea in mod concis continutul. Fiecare coloana si fiecare rand va preciza itemii continutului.
Coloanele se pot subdevide in subcoloane. Atat coloanele cat si randurile pot avea la sfarsit un total (insumarile se fac, de regula, pentru date de acelasi fel).
Reprezentari grafice
Datele sistematizate pot fi prezentate si sub forma grafica. Reprezentarile grafice permit o examinare intuitiva a rezultatelor si inlesnesc adeseori comparatii prin suprapunerea mai multor curbe pe aceeasi figura.
Cand rezultatele obtinute sunt grupate doar in cateva categorii sau procente se folosesc diagrame de structura si diagrame de comparatie.
|
|
Diagrama de structura se utilizeaza mai ales cand se reprezinta partile unui intreg. Sectoarele se calculeaza dupa unghiul lor, folosind regula de trei simpla. Daca 100% reprezinta 3600 atunci 60% reprezinta x.
![]()
|
|
Diagramele de comparatie constau adeseori in coloane paralele avand aceeasi baza sau latime si alaturat o scala de marime
Cand vrem sa reprezentam grafic o serie de variatie ne folosim de sistemul de referinta al axelor rectangulare.
|
|
X f
3 – 5 3
6 – 8 5
9 – 11 9
12 – 14 16
15 – 17 10
18 – 20 4
21 – 23 3
Poligonul si curba de frecvente fac posibila precizarea formei pe care o are distributia studiata. De asemeni compararea grafica a unor linii paralele.
Distributia statistica
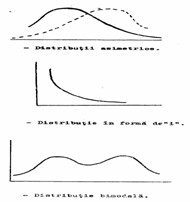
Valorile obtinute in cercetare se grupeaza dupa frecvente in curbe de distributie de forme diferite. Acestea pot fi distributii normale si distributii asimetrice.
Distributiile normale se prezinta sub forma profilului unui clopot. Ele sunt distributii simetrice; valorile frecventelor situate de o parte si de alta a clasei cu frecventa maxima sunt egale sau difera foarte putin intre ele. O astfel de curba se obtine numai atunci cand datele obtinute sugereaza astfel de ipoteza si este caracteristica fenomenelor aleatoare.
In cazul distributiilor asimetrice majoritatea frecventelor se spre dreapta sau spre stanga medianei.
In cazul distributiilor in forma de i curba frecventelor este constant descrescatoare. De exemplu, curba erorilor, in seria exercitiilor pentru formarea deprinderii este constant descrescatoare; distributiile in forma de j au frecvente crescatoare.
In anumite cazuri putem intalni distributii avand frecventele mai mari in doua grupe; este vorba de o distributie sinusoidala, care sugereaza ipoteza existentei a doi factori sau grupe diferite.
Verificati-va cunostintele:
tabele si grafice;
digrame de structura.
BIBLIOGRAFIE:
1.Alban, P., Les Questionnaires psychologiques. Paris, P.U.F., 1968.
2.Alexe, N.,Cercetarea stiintifica in domeniul educatiei-fizice. In: Educatia Fizica si sport, nr.4 / 1991.
3.Alexe, N., Probleme actuale si de perspectiva ale cercetarii stiintifice in domeniul educatiei fizice si sportului. In Educatia fizica si sport, nr.2 / 1976.
4.Antonelli, F., Metoda convorbirii psihologice a sportului, C.N.E.F.S., 1971.
5.Apostol, P., Educatia si pedagogia in perspectiva operationala, Bucuresti, E.D.P., 1969,
6.Apostol, P., Metodologia: modelarea actiunii educationale. In: Fundamente pedagogice, vol. II, (sub. red.): Tudoran, D.; Vaideanu, G., Bucuresti, E.D.P., 1970.
7.Bazele informaticii documentare, vol. I-II, Consiliul National de Informare si Documentare, Bucuresti, 1976.
8.Bernal, J.D., Stiinta in istoria societatii, Bucuresti, Editura Politica, 1964.
9.Beveridge, W.I., Arta cercetarii stiintifice, Bucuresti, Editura stiintifica, 1968.
10.Brooke, J.B., Psihologia sportului si studiul miscarilor umane. Definirea domeniului profesional de specialitate si academic universitar. In: Epuran, M., (sub.red.), Psihologia si sportul contemporan, Bucuresti, Editura Stadion, 1974.
11.Coler, D., Butoi, T, Testul in educatie fizica si sport. In: Educatie
fizica si sport, nr. 10 / 1973.
12.Derek, I., Stiinta mica, stiinta mare. Bucuresti, Editura stiintifica, 1971.
13.Donskoi, D., Biomecanica, bazele tehnicii sportive. Bucuresti, Editura Stadion, 1973.
14.Dragan, I., Locul anchetelor de opinie in investigatia sociologica si psihologie sociala. Col. Teorie si metoda in stiintele sociale, vol. 6, Bucuresti, Editura Politica, 1968.
15.Dumitrescu, D., Trepte spre stiinta, Cluj, Editura Dacia, 1974.
16.Epuran, M., Despre reprezentarile miscarilor in invatarea exercitiilor fizice. In: Revista de pedagogie, nr. 6, 1958.
17.Epuran, M., Psihologia educatiei fizice, Bucuresti, Editura Sport-Turism, 1976.
18.Epuran, M., Metodologia cercetarii activitatilor corporale, Vol. I si II, Bucuresti, 1992.
19.Flonta, M., Problema acordului structurilor matematice cu datele experientei. In: Teorie si experiment, Vol. XIV, Bucuresti, Editura Politica, 1971.
20.Georgescu, St., Epistemologie, Bucuresti, E.D.P., 1978.
21.Hoffman, O., Sisteme conceptuale operationale in sociologie, Bucuresti, Editura stiintifica si Enciclopedica, 1977.
22.Kornin, P.V., Bazele logice ale stiintei, Bucuresti, Editura Politica, 1977.
23.Lantos, St., Valoarea euristica a previziunii stiintifice. Teza de doctorat. Universitatea Babes-Bolyai, Cluj-Napoca, Facultatea de Istorie-Filosofie, 1969-1970.
24.Lazarescu, G., Introducere in metoda de indexare coordonata, Academia R.S.R., Centrul de Documentare stiintifica, Bucuresti, 1966.
25.Marolicaru, M., Abordarea sistematica in educatia fizica, Cluj-Napoca, 1992.
26.Margineanu, N., Psihologia logica si matematica, Cluj-Napoca, Editura Dacia, 1975.
27.Margineanu, N., Natura stiintei, Bucuresti, Editura stiintifica, 1968.
28.Mic dictionar enciclopedic, Bucuresti, Editura stiintifica, 1986.
29.Mihailov, A.I., si colab. Informatica documentara, Bucuresti, Editura Stiintifica, 1970
30.Moser, C.A., Metodele de ancheta in investigarea fenomenelor sociale, Bucuresti, Editura stiintifica, 1967.
31.Pacczolay, G., Tudomŕnyok és rendszerek -Tudomŕnyterületek közös törvényszerüségei, Budapest, Akadémiai Kiado, 1973.
32.Pantin, C.A., Raporturile dintre stiinte, Bucuresti, Editura Enciclopedica Romana, 1972.
33.Popa, C., Teoria cunoasterii in perspectiva semiotico-praxiologica asupra actului cunoasterii, Bucuresti, Editura stiintifica, 1972.
34.Pieron, M., Analyse del'enseignement des activités physiques. Ličge. Université de Ličge au Sort Tilman, 1980.
35.Radut, C., Morfometria specifica - instrument specific de pregatire si selectie in sport, In: Educatie fizica si sport, nr.1 / 1981.
36.Radu, I., Introducere in psihologia experimentala si statistica, Bucuresti, Editura Didactica si Pedagogica, 1967.
37.Rokusfalvy, P., Importanta conceptiei moderne de cercetare si practica psihologiei sportului. In: Epuran M., (sub.red.) Psihologia si sportul contemporan, Bucuresti, Editura Stadion, 1974.
38.Rosca, Al., Metodologie si tehnici experimentale in psihologie, Bucuresti, Editura stiintifica, 1971.
39.Rosca, Mariana, Metode de psihodiagnostic. Bucuresti, Editura
Didactica si Pedagogica, 1972.
40.Savinov, A.V., Legile logice ale gandirii, Bucuresti, Editura stiintifica, 1961.
41.Sahleanu, V., Etica cercetarilor stiintifice, Bucuresti, Editura stiintifica, 1967.
42.Tövissi, Berta, Rolul modelelor in invatarea exercitiilor de gimnastica sportiva. In: Educatie fizica si sport, nr. 7 / 1975.
43.Tövissi, Berta, Utilizarea simbolurilor figurale ca modele de invatare a exercitiilor de gimnastica. In: Educatie fizica si sport,nr.8/19
|
Politica de confidentialitate |
| Copyright ©
2025 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |