
Dezvoltarea capacitatilor de explorare investigare la scolarul mic, prin rezolvare de probleme
b. Partea I:
PARTICULARITATILE PSIHOLOGICE ALE SCOLARULUI MIC
In jurul varstei de sapte ani, se deschide o alta perioada a existentei - in viata micutului are loc un eveniment deosebit de important - intrarea in scoala, fapt ce duce la o considerabila expansiune a universului copilului pe plan mental.
Dat fiind faptul ca orice copil care intra in scoala are cel putin un an sau doi de experienta in gradinita, noutatea consta in faptul ca mediul scolar il modifica destul de brutal pe cel prescolar; copilul trebuie sa se adapteze pe loc unor constrangeri inevitabile pe care nu le-a cunoscut de-a lungul dezvoltarii lui si inaintea carora puterea farmecului si afectiunii atat de eficienta acasa, da gres.
Intrarea in scoala constituie pentru micut descoperirea vietii sociale, publice si profesionale, intra in societate alaturi de covarsnici si face parte dintr-un grup in care este egal ca varsta, posibilitati fizice si mentale cu partenerii sai. De acum inainte se masoara cu cei de o seama fara sa se mai confrunte cu fiinte care il depasesc. Copilul are acum ocazia sa-si stabileasca singur statutul si raporturi de reciprocitate cu cei egali lui. Societatea in care se integreaza capata tot atata importanta ca si familia pe care la un moment dat o poate eclipsa. Tendinta de a se conforma standardelor grupului intrece cu mult tendinta de a se conforma dorintelor adultului.
Are loc in aceasta perioada o crestere treptata a unor caracteristici proprii copilariei de care am vorbit mai sus si aparitia unei noi atitudini mai controlate si mai mature fata de sarcinile de invatare. Invatarea scolara are acum un alt continut, cadru si mod de desfasurare prin care se deosebeste de toate celelalte acte de invatare anterioare. Hotaratoare pentru viitorul fiecarui copil sunt acum volumul, calitatea si diversitatea continuturilor invatarii scolare.
Cunostintele care se acumuleaza acum sunt gradate si complexe capabile sa formeze capacitatii psihice de baza, deosebit de semnificative pentru urmatoarele etape, pentru viitorul profesional, chiar pentru toata viata. De aceea trebuie sa existe o stransa legatura intre scoala si familie si impreuna sa sprijine dezvoltarea Tuturor posibilitatilor acestui stadiu.
Spre deosebire de celelalte stadii acum se stabilesc relatii obiective cu lumea, scoala atragandu-l pe copil in sfera rationalului, inteligibilului, rigorilor cunoasterii, se formeaza deprinderi intelectuale de baza in ceea ce priveste citit - scrisul operarea cu simbolurile matematice, etc.; are loc un fel de maturizare a tuturor manifestarilor : psiho - comportamentale, isi asimileaza statutul de elev, se schimba pozitia in cadrul familiei si creste interesul pentru reusita si succesul scolar. In final are loc un echilibru general stabil in raporturile cu mediul, implinindu-se toate atributele copilariei.
Dezvoltarea sociala si cea intelectuala sunt acum principalele aspecte ale cresterii personalitatii caracterizata prin destramarea mentalitatii infantile si spargerea cadrului familial. Aceasta dezvoltare se sprijina pe o miscare continua, fina, controlata, pe o activitate navalnica si o intensa expansiune creatoare. Gesell caracteriza fiecare din aceste varste ca fiind: "sase ani, varsta extremismului, a tensiunii si agitatiei; sapte ani, varsta calmului, a preocuparilor interioare, a meditatiei; in care apare oentru prima data « iterioritatea », una din trasaturile stadiului urmator; opt ani, « varsta cosmopolita », a expansiunii, a extravagantei, a interesului universal; in sfarsit noua ani, varsta autocriticii, a autodeteminarii, varsta clasificarilor si a recensamintelor generale, in care se manifesta transformarile ce vor duce la individualismul temperat din etapa ulterioara. '
In jurul varstei de sapte ani, se formeaza o multime de capacitati intelectuale, afective, volitionale, deprinderi generale de autoservire, reguli de conduita si o receptivitate si sensibilitate mentala ce garanteaza organizarea unor capacitati si disponibilitati psihice care vor permite desfasurarea unei activitati complexe, cum este cea scolara.
Pentru a fi capabil de randament scolar, copilul mic are nevoie de un regim corespunzator de hrana si odihna. In lipsa acestuia apar dificultati in procesul de invatare cum ar fi: stari de somnolenta, dificultati de concentrare a atentiei, slabirea interesului pentru activitatile din clasa.
Un alt moment foarte important pentru scolarul mic este realizarea temelor pentru acasa care ar trebui sa se desfasoare in prezenta parintilor si daca se poate la aceleasi ore pentru a se forma obisnuintele corespunzatoare, instalandu-se mai usor atentia si tonusul general necesar, se mobilizeaza cunostintele anterioare si procedeele de lucru. Totusi parintii nu trebuie sa substituie elevul, ci sa urmareasca dezvoltarea progresiva a autonomiei in lucru, mentinandu-si interesul pentru ce si cum face copilul, valorizandu-i munca. Acestia trebuie sa manifeste interes pentru activitatea scolara a copilului sustinand si valorizand eforturile copilului .
In realizarea sarcinilor scolare copilul are nevoie de pauze care sa-i satisfaca trebuintele de miscare si relaxare asigurandu-i un bun tonus mintal pentru ceea ce urmeaza.
Cea mai importanta activitate a scolarului ramane, totusi cea petrecuta in clasa, ceea ce implica o atentie deosebita din partea familiei si invatatoarei pentru a preveni si inlatura eventualele disfunctionalitati ce pot aparea la aceasta varsta care ar putea genera atitudini negative fata de scoala si ar compromite efectele formative ale acesteia.
Prima intalnire cu scoala poate lasa urme placute sau neplacute dupa cum am aratat in partea de inceput a prezentei lucrari, urme ce pot sa influenteze lent starile copilului. Contactul cu scoala poate fi dupa cum spunea Debesse "un al doilea soc dupa cel al nasterii'. Adaptarea copilului la acest mediu presupune integrarea in programul scolar si in activitatile sale, realizarea unei relatii noi cu invatatoarea, soabilirea unor relatii cu cei care ii devin colegi si cu care se va confrunta tot timpul a se va compara in primul rand dupa criteriul calitatii prestatiei scolare.
Transformarile organice si in special cele ale sistemului nervos impreuna cu influentele mediului scolar si ale invatarii sistematice au ecou in toate planurile vietii psihice a copilului: in cognitie, afectivitate, motivatie, vointa si personalitate.
Intre 7 si 8 ani, dezvoltarea psihica este intr-un stadiu de echilibru care conduce catre activitati de concentrare, un prilej foarte bun pentru asimilarea si completarea cunostintelor. El judeca , este interesat de sensul logic al situatiilor problematice in care se afla uneori si foloseste foarte mult guma, lucru care A.Gesell il atribuie dezvoltarii simtului critic al copilului. Folosirea gumei pune in evidenta de asemenea si dezvoltarea capacitatilor legate de perseverenta, ca trasatura in plina constituire. La 7 ani elevul cunoaste ceasul, anotimpurile, lunile, este retinut, foarte intuitiv si respectiv, deschis la fenomenele de cultura .
Desi este strans legat afectiv de mama, el manifesta intens si disponibilitate si fata de alte persoane, in special fata de invatatoare care imbina dragostea cu existenta si le manifesta in mod egal fata de copii. Ea formuleaza cerinte clar si exigent, pe care elevii le indeplinesc, apoi in functie de rezultat isi arata multumirea sau nemultumirea. Invatatoarea urmareste in mod constant sa asigure insusirea cunostintelor, formarea de deprinderi si capacitati amplificandu-si rolurile de indrumare, control, verificare si evaluare. In clasa I copiii o percep ca pe un lider al grupului lor care trebuie sa stie ce si cum se face si toti ii comunica totul, ii aduc flori, dezvolta o afectiune de tip simbiotic .
La varsta de sapte ani sociabilitatea este relativ complexa - copilul este atent, face mici servicii care nu sunt prea izolate si nu-l rapesc prea mult de la activitatile ce - i fac placere in mod spontan. Este foarte sensibil si uneori are accese de plans sau stari plangacioase. Fenomenul acesta se manifesta si in relatiile de joc cu covarsnicii care au un rol formativ pentru dezvoltarea psihica a individului. Oricat ar fi de bune relatiile copilului cu adultul, ele nu pot satisface toate nevoile de dezvoltare ale acestuia. Impartirea copiilor pe clase se face dupa criterii de varsta si particularitati psihice asemanatoare care permit functionarea grupului si exercitarea rolurilor sale cu afecte formative crescute.
Chiar daca a fost in gradinita, copilul descopera cu adevarat grupul la intrarea in scoala cand dezvoltarea mintala si experienta personala ii permit sa fie atent la cei din jur si sa se integreze cu adevarat in grup. Sub permanenta indrumare a invatatoarei ei sunt atrasi sa colaboreze intr-o activitate importanta si sa obtina rezultate semnificative si de durata pentru ca apoi sa-si masoare fortele cu ceilalti si sa dobandeasca un loc intre ei . Pe parcurs grupul se maturizeaza, isi stabileste norme care trebuie respectate de toti membrii sai si exercita presiuni asupra acestora pentru a le indeplini, a-si atinge scopurile si realiza programele. Copilul sanatos din punct de vedere psihic se integreaza la timp si usor grupului spre deosebire de cel cu trasaturi patologice care are dificultati de integrare, intarzie sa adere la grup, e izolat, insingurat, tensionat, multumit. Tratamentul dur din partea grupului poate provoca intr-o structura atat de fina a personalitatii in plina formare, adevarate mutilari sufletesti .
1. DEZVOLTAREA PERCEPTIILOR SI A CAPACITATILOR DE OBSERVARE
Activitatile scolare antreneaza principalele modalitati senzoriale: vazul, auzul, sensibilitatea tactil - chinestetica. Toate acestea cresc foarte mult in acest stadiu fata ce stadiul anterior ( vazut cu 60 % iar capacitatile de diferentiere a stimulilor cu 45 %). 'Se consolideaza schemele perceptive, care vor permite identificarea rapida a obiectivelor sau a literelor si cuvintelor in citire, culorile sunt mai bine diferentiate si verbalizate si la fel formele' ( M. Zlate, 1999, p 111 ).
Se perfectioneaza functia auzului, in special cel fonematic, acesta fiind cel mai mult solicitat si dezvoltat in legatura cu insusirea citit - scrisului.
Sensibilitatea si perceptiile tactile au si in aceasta perioada un rol foarte mportant in cunoasterea obiectelor, elevii fiind tentati sa atinga tot ceea ce se afla in raza lor vizuala. Aceste explorari perceptive devin acum mai organizate si mai sistematice sub influenta scolii .
Perceptia la distanta se afla in prim progres intre varstele de 8 si 9 ani, copilul aflandu-se intr-o faza de expansiune si de extrovertire. Este rapid, are o atitudine " manifest euforica ' si foloseste frecvent superlativele in vocabular. Toate acestea sunt rezultatul progresului inregistrat in dezvoltarea personalitatii si a cresterii curiozitatii copilului fata de tot ceea ce il inconjoara.
Ca o concluzie a celor prezentate se poate spune ca sub influenta scolii creste caracterul intentionat al activitatilor perceptive, viteza de explorare a lucrurilor, se stabilizeaza schemele perceptive, perceptia servind mai bine activitatilor de invatare sau celor lucrative, continuturile de invatare scolara si sarcinile ce sunt indeplinite de copii ii pun in contact cu multe aspecte ale realului si imbogatesc semnificativ experienta perceptiva a copiilor; includerea sistematica si constanta a perceptiei in activitatile de invatare schimba raporturile sale de pana acum cu gandirea si ii sporeste eficienta. Perceptia nu mai subordoneaza gandirea ci este insasi subordonata si suporta influentele acesteia.
Activitatile observative ale scolarului mic beneficiaza de acum de noua relatie cu gandirea si de influentele sistematice si de durata ale invatarii - lucru care nu se intampla in stadiul anterior si care constituie o conditie importanta a eficientei cunoasterii. Copiii sunt mult mai activi si au multe cunostinte ce le asigura centificari rapide si interpretari ale celor percepute. Totusi, aceste activitati de observare trebuie organizate si indrumate de catre invatatoare pentru a avea eficienta ceruta. Acest lucru va avea efecte importante pentru dezvoltarea capacitatilor observative necesare invatarii din urmatoarele stadii.
2. DEZVOLTAREA REPREZENTARILOR LA SCOLARII MICI
Cercetarile de pana acum arata ca in perioada celei de-a treia copilarii actioneaza o lege importanta, ontogenetica a activitatii psihice, si anume aceea ca orice intelegere presupune cu obligativitate organizarea ei initiala ca reprezentare, ca intuitie.
Capacitatea de a lucra activ cu reprezentarile se dezvolta tocmai datorita acestui fapt. Pentru a intelege profund fenomenele, copilul se sprijina pe acele tipuri de reprezentari care s-au format in contactul nemijlocit si permanent cu realitatea inconjuratoare .
Activitatea scolara insa nu se limiteaza la experiente individuale. Elevul aude de plante si animale pe care nu le-a vazut niciodata, de evenimentele istorice vechi, acestea devenind cunostinte care se materializeaza in reprezentari noi.
Sub influenta procesului de insusire a unor cunostinte elementare de matematica, stiintele naturii, istorie, geografie, etc.,creste volumul si varietatea reprezentarilor. Cititul-scrisul la clasa I, dezvolta o categorie aparte de reprezentari, cele fonetice si cele grafice, care vor fi o conditie a perfectionarii scris-cititului.
Daca elevul are deja reprezentarea unui cuvant scris, el rezolva mai bine sarcinile scrierii dupa dictare fara sa se opreasca prea mult asupra analizei grafemelor sale. Reprezentarile geometrice accesibile scolarilor mici se stabilizeaza si devin operative si se formeaza si cele topografice care sunt consolidate prin exercitii speciale.
Datorita acestei dezvoltari cognitive generale, copii pot avea acum nu numai imagini reproductive statice, ci si cinetice si de transformare. Ei pot sa reconstituie pozitiile intermediare ale unui corp in miscare numai daca l-au perceput o data miscandu-se. Incep sa se realizeze mai usor si imaginile anticipative ce vor fi implicate in desfasurarea imaginatiei sau in intelegerea unor relatii mai dificile atunci cand isi insusesc diferite cunostinte.
Reprezentarile au o mare pondere in activitatea mintala avand un rol deosebit in formarea notiunilor. " Procesarea informatiilor la nivelul mecanismelor reprezentarii este obligatorie in acest stadiu. Formarea lor este un scop principal al multor lectii de la fiecare disciplina. Sub influenta scolii ele castiga claritate, coerenta, mobilitate si ajung la un grad de generozitate si sprijina insusirea autentica a notinunilor si operarea corecta cu acestea.'( T. Cretu 2000 , p 76)
4. DEZVOLTAREA LIMBALULUI
Achizitia limbajului trebuie sa aiba in vedere, pe parcursul tuturor stadiilor primului ciclu al dezvoltarii psihice, volumul vocabularului, particularitatile vorbirii, scris-cititului si ale limbajului intern si a rolurilor sale speciale.
Cand vine in clasa I, un copil care a avut conditii normale de dezvoltare; comunica foarte bine tot ce este legat de varsta lui sau activitatile ce le desfasoara. Pentru limba materna este foarte important si bine dezvoltat auzul fonematic, iar perceptiile auditive se desfasoara operativ asa incat cele comunicate sunt receptionate rapid si decodificate. La toate acestea se asociaza memoria auditiva care pastreaza -reprezentarile fonetice si semnificatiile si ajuta la recunoasterea rapida a cuvintelor .
Cand deprinderile de vorbire sunt foarte bine consolidate pentru comunicarea obisnuita, debitul verbal este crescut iar mesajul are coerenta si expresivitate.
La scolarii mici vorbirea se sprijina pe structuri verbale pe care le preia prin imitatie de la adultii din familie sau achizitionate in gradinita in care sunt implicate: normele gramaticale ce controleaza fluxul verbal.
Odata cu invatarea scris-cititului procesul vorbirii va avea o noua calitate. In acest proces sunt antrenate perceptiile, reprezentarile, gandirea dupa cum urmeaza: perceptia este conditie si efect al invatarii, iar gandirea este implicata in intelegerea contextului exprimat prin simbolistica literelor. Invatarea citit-scrisului are la baza dezvoltarea capacitatii de a diferentia sunetele care compun cuvintele din punctul de vedere auditiv si chinestezico-vizual. Aceste diferentieri se formeaza pe baza unei analize constiente si rationale ce consta in compunerea si descompunerea cuvintelor si a propozitiilor - ceea ce se numeste in limbajul practicienilor metoda fonetica analitico -sintetica. Urmand o asemenea cale, elevul ia cunostinta de faptul ca orice cuvant este format din sunete si grupuri de sunete numite silabe care pot fi grupate sau separate.
Invatarea citirii presupune antrenarea multor functii si procese psihice elaborandu-se un adevarat complex vizual - verbal - motor. Vazul este cel mai important deoarece asigura discriminarea sunetelor grafice si cunoasterea lor. Deasemenea, cu cat se perfectioneaza miscarea ochilor cu atat are loc o percepere operativa si facilitarea intelegerii celor citite. Se produc si miscari de regresie si de anticipare asfel ca pe masura ce se perfectioneaza cititul, anticiparea cu privirea a semnelor ce urmeaza este si mai larga, cuprinde mai multe litere sau cuvinte. (Psihologia educatiei si rjezToltarii , 1983 , p . 79 ) . Mialaret care s-a ocupat in principal de aceasta problema constata ca la copiii din clasa a II a, care citesc mai slab, aceasta depasire a cuvantului citit este de numai 4-5 litere, iar la cei foarte buni este de 11 elemente
Din experienta mea la clasa pot spune ca in procesul citirii copiii fac unele greseli tipice cum ar fi "inlocuiri' dupa sens, asemanare sau sonoritate, repetari si simplificari de cuvinte.
Din punctul de vedere al modului cum citesc sunt copii care citesc greoi si retin putin din sens, copii care citesc greoi, dar retin bine sensul, copii care citesc usor a retin bine sensul si copii care citesc usor si retin putin sensul ( Ursula Schiopu . p 2 ). Aceste situatii cer un ajutor diferentiat din partea invatatoarei.
Conditiile de baza ale citirii sunt dupa A . Leroy -Bonsion si R . Ligeti auzul fonematic, capacitatea de analiza si sinteza a sunetelor verbale discriminarea vizuala a formelor, sinteza silabicii, memoria vizuala si auditiva, particularitati ale afectivitatii motivatiei si vointei.
La randul sau, scrierea presupune si ea antrenarea unor capacitati senzorial -perceptive si motrice dar si procese mentale.
Premisele neurofunctionale ale insusirii scrisului sunt urmatoarele: stabilizarea laterabilitatii functionale a emisferelor cerebrale, maturizarea schemei corporale, perfectionarea perceptiilor spatiului in raport cu fiinta proprie, discriminarea formelor in spatii mici, distingerea caracteristicilor identice si a celor simetrice.
Dat fiind faptul ca la inceput componenta verbal - motorie este strans legata de componenta verbal - auditiva, in timpul scrierii si al dictarii copiii isi dicteaza in soapta. Am incercat la elevii mei din clasa I sa le interzic sa nu - si mai miste buzele in timpul scrierii dar rezultatele au fost mult mai slabe decat de obicei .Chiar copiii foarte buni au facut numeroase greseli.
Insusirea citit - scrisului impreuna cu asimilarea multor cunostinte duc la imbogatirea vocabularului. La sfarsitul clasei a IV a, vocabularul pasiv contine 4 -4500 de cuvinte iar cel activ 1500-1600; se imbogateste semnificatia cuvintelor si copiii pot descoperi mai usor sensurile figurate ale unor expresii verbale.Competenta lingvistica, performantele exprimate in capacitatea de a dialoga, a povesti o se exprima in scris, ale scolarului mic sunt acum intr-un real progres fata de stadiul anterior.
In scolaritatea mica, limba este obiect de studiu, se insuseste constient si voluntar sub conducerea invatatoarei si contribuie la progresul tuturor capacitatilor cognitive ale copilului.
MEMORIA SCOLARULUI MIC
Memoria are un rol deosebit de important in procesele de adaptari, in dezvoltarea activitatii intelectuale si practice, in dezvoltarea generala a activitatii psihice.
Copilul mai pastreaza inca din insusirile memoriei din perioada prescolaritatii. Memoria lui se sprijina pe perceptibil, pe ceea ce 1-a impresionat mai mult. Acest lucru face apel la o fixare concret-senzoriala prin intermediul materialului didactic, al ilustratiilor pentru ca fixarea si pastrarea cunostintelor sa se faca mai usor. Memorarea copilului abia intrat in clasa I este fragmentara si insista de multe ori asupra elementelor nesemnificative si neesentiale deoarece este legata de predominarea analizei, a concretului, a fragmentului perceput. Insa procesul continuu de maturizare neurofunctionala si antrenarea constanta in activitatea de invatare sistematica schimba calitativ memoria de-a lungul timpului.
In primul rand creste caracterul activ al desfasurarii procesului de intiparire; memoria logica are o pondere mai mare in rezolvarea tuturor sarcinilor de invatare, deci exista o legatura stransa a memoriei cu gandirea; progreseaza foarte mult memoria voluntara pe masura ce copilul intelege relatia dintre rezultatele sale in clasa si efortul de a invata. In a doua parte a stadiului, clasele a III a si a IV a copiii fac dovada existentei unei metamemorii spontane, adica isi modeleaza memoria voluntara in raport cu specificul sarcinilor. Tot catre sfarsitul stadiului incep sa se utilizeze criterii logice de organizare a materialului de invatat. In privinta pastrarii in memorie daca la clasele I si a II a invatatoarea este cea care organizeaza repetitiile si le esaloneaza in functie de volumul si dificultatea materialului, la clasele a III a si a IV a elevii isi dau seama de necesitatea repetarii din cand in cand a celor invatate.
Din punctul de vedere al productivitatii memoriei se poate spune ca incep sa apara unele particularitati individuale in functie de care elevii se pot diferentia intre ei in ceea ce priveste usurinta intipariri, durata pastrarii si eficienta reproducerii . Astfel sunt copii care invata repede si tin minte mult timp si actualizeaza cat mai complet cei cu performante foarte bune in invatare; altii invata greu dar pastreaza multa vreme ce au achizitionat si actualizeaza bine; elevii care invata usor dar uita repede iar rezultatele lor la invatatura sunt fluctuante si cei care invata greu si uita repede.
6. IMAGINATIA SI PARTICULARITATILE EI
In perioada celei de-a treia copilarii se asigura cateva conditii de baza in scopul dezvoltarii capacitatilor imaginative: copilul acumuleaza o experienta personala de viata si cunostinte elementare din diverse domenii care pot alimenta combinatiile native; creste interesul pentru observarea mediului inconjurator, a oamenilor iar preocuparile lor alimenteaza si chiar stimuleaza chiar demersurile imaginative. Cresc mult capacitatile mintale care il determina pe copil sa priveasca in mod mai obiectiv lumea; sunt stapanite mai bine deprinderile de scris-citit, desen, constructii etc.. Activitatile din clasa, jocul si preocuparile din timpul liber sunt si ele stimulente surse de transformari imaginative. (T. Cretu , 2000 , p .86 )
In desfasurarea tuturor lectiilor, cu precadere cele de istorie, geografie, mediu inconjurator este antrenata imaginatia reproductiva care sprijina mai buna intelegere a cunostintelor sau aplicarea lor in situatii noi . Aceasta este deosebit de utila in dezvoltarea gustului pentru lectura.
Imaginatia creatoare la scolarii mici a generat puncte de vedere contrarii. In primele doua clase copilul manifesta fantezii reduse in exercitarea educatiei plastice, a modelajului, colaje. El are si un spirit critic ridicat fata de propriile lucrari deoarece evalueaza mai sever din punctul de vedere al recognoscibilitatii ca forma. Fantezia e totusi sa gaseasca domenii noi de exercitare. Se formeaza treptat, catre mijlocul stadiului ( 8-9 ani ) capacitatea de a compune, se dezvolta capacitatea de a povesti si de a crea povestiri cu intriga de actiune, abilitatea de a folosi elemente descriptive literare. Spre 9-10 ani plansa de la educatie plastica devine mai incarcata 'atmosfera' - pomii, casele, persoanele sunt puncte de plecare pentru individualizari de teme, se castiga tehnica redarii elementelor de perspectiva si adesenarii suprapuse a obiectelor din desen .
SPECIFICUL ATENTIEI SCOLARULUI MIC
Pe parcursul acestui stadiu copilul mic dobandeste cateva calitati ale atentiei care-sunt absolut necesare pentru dezvoltarea lui interioara.
In primul rand am sa amintesc ca la intrarea in clasa I domina atentia involuntara dar pe parcursul urmatoarelor clase este mai frecvent prezenta cea voluntara si din ce in ce mai eficienta. Prin toate activitatile pe care le desfasoara la clasa, invatatorul consolideaza si amplifica mecanismele de reglaj voluntar in concordanta cu cerintele puse in fata copilului. Tot acum domina si atentia externa (la inceputul scolii ) dar, treptat, gandirea si memoria sunt din ce in ce mai antrenate, se manifesta frecvent atentia interna, bazata pe desfasurari mintale mai mult sau mai putin complexe. Stabilitatea creste si ea de la 25 de minute la inceputul scolii la 40 - 45 de minute sub influenta anilor de scoala sustinand si invatarea independenta de dupa ore sau alte activitati din timpul liber.
In timpul primilor 4 ani de scoala se modifica si volumul atentiei de la 2 - 3 elemente receptionate simultan si in timp foarte scurt la 4 - 5 elemente, copilul fiind capabil sa citeasca un cuvant si sa prinda in campul sau vizual si pe cel care urmeaza, usurand astfel intelegerea ideii cuprinsa intr-o fraza iar apoi in text.
Distributivitatea nu sta nici ea pe loc si ajuta pe loc copilul sa receptioneze si ceea ce i se explica si ceea ce i se arata .
Intr-un real progres se afla si capacitatea de concentrare a atentiei, dar mai sunt inca insuficiente in manifestarea ei in sarcinile dificile sau atunci cand intervine oboseala. In clasa I atentia elevului poate fi foarte usor distrasa de schimbari neasteptate si uneori neinsemnate in ambianta si in aceste conditii ei pot sa nu receptioneze mesajele, sa nu realizeze ce se cere. Tot acum , trebuie mentionat si faptul ca ei nu reusesc sa-si modeleze gradul de concentrare a atentiei in functie de momentele unei activitati si se poate sa fie neatenti chiar in cele mai importante secvente pentru realizarea continutului lectiei sau in momentul comunicarii temelor pentru acasa
Vorbind despre toate aceste lucruri ne dam seama ca este foarte important sa descoperim elevii care au dificultati speciale de atentie si sa aplicam tratamentul corespunzator Aceste dificultati speciale sunt urmatoarele neatentie activa si pasiva care este mai greu de relevat pentru ca elevul respectiv este linistit in aparenta si e creea impresia ca urmareste ceea ce se petrece in clasa pare sa lucreze ce s-a cerut dar in realitate sa se afle cu mintea in alte locuri
Asigurarea dezvoltarii corespunzatoare a atentiei in acest stadiu este o contributie majora a ciclului primar la pregatirea pentru indelungatul proces de invatare din urmatoarele stadii T Cretu p
CARACTERISTICILE DEZVOLTARII AFECTIVITATII
Aceste mecanisme cognitive asigura o invatare eficienta doar daca sunt sustinute cele orientativ-stimulative si reglatorii, fapt pentru care continui cu o caracterizare a copilului si din aceste puncte de vedere.
In acest stadiu, evolutia afectivitatii intra intr-o stare de " latenta ' spun autorii orientare psihanalitica, in cursul careia libidoul se orienteaza catre toate partile organismului sustinand implicarea copilului in diverse activitati si mai ales in cele scolare. P . Osterrieth subliniaza si ea ca in aceasta perioada dezvoltarea intelectuala si cea sociala o eclipseaza pe cea afectiva.
Totusi, din experienta mea la clasa am constatat ca latura afectiva joaca un rol deosebit de important mai ales in prima perioada a scolaritatii cand copilul este de receptiv si sensibil. El simte cand este privit cu incredere, cu dragoste si nu, de aceea reactia lui fata de cei mari este diferita.
Omul este o fiinta rational - afectiva. El este un mare producator si consumator de afectivitate. Energia psihica si afectiva a invatatoarei este receptata de scolar si are implicatii asupra sanatatii afective si biopsihice dar si asupra randamentului scolar. Iubirea, dorul, regretul, mila, extazul, nostalgia, sentimentele intelectuale, morale, estetice, religioase sunt sentimente specific umane care se cultiva doar daca cel care este cultivator le are si le aplica adecvat. Caci nu se poate cultiva dragoste prin ura si nici pacea prin razboi.
Se tot spune ca micutul traieste o adevarata " intarcare afectiva ' odata cu intrarea in scoala unde nu mai sunt potrivite conduitele anterioare. Este foarte adevarat pentru ca incertitudinile, nesiguranta, tatonarile tind sa domine si astfel nu stie daca sa se bucure sau sa se intristeze de inceperea scolii, daca sa fie atras de scoala sau sa se teama de ea, sa fie incantat de noii colegi sau dezamagit, daca ii place sau nu invatatoarea. Am intalnit copii carora nu le placea invatatoarea si rezultatele lor scolare au fost un esec .
U. Schiopu considera ca se produce acum un fel de reversibilitate afectiva, fapt care pregateste maturizarea copilului ( U. Schiopu , E. Vrza , 1995, p.165 ). Si in procesul de formare a unor atitudini noi cerute de scoala se produce tot un fel de reversibilitate. Copilul oscileaza intre a fi ascultator dar si neastamparat, zgomotos, intre a fi atent si politicos si agresiv etc..
Dezvoltarea cognitiva si desfasurarea in bune conditii a procesului instuctiv-educativ duc la imbogatirea si diversificarea trairilor afective. Copilul simte ca este fericit traieste emotia succesului, satisfactia invingerii dificultatilor, bucuria obtinerii aprecierii tuturor celor care il inconjoara daca familia si scoala il apreciaza pentru activitatea pe care el o desfasoara, se mandresc cu el, il incurajeaza, este privit cu admiratie. In cazul acesta scolarul a pasit cu succes pe drumul lung al invatarii. Scoala pentru copil ar trebui sa fie totdeauna terenul realizarii de sine. In scoala pot fi incercate si trairi negative din diferite motive care nu pot fi evitate in mod absolut dar este de dorit evitarea repetarii lor pentru a nu se stabili o legatura neplacuta cu scoala care sa genereze efecte dezadaptative atat in clasele primare cat si in urmatoarele perioade ale vietii.
In acest stadiu se cristalizeaza unele sentimente noi si complexe generate de noile sale activitati si relatii, iar la scurt timp dupa inceperea scolii se constata o crestere evidenta a capacitatii de autocontrol asupra conduitelor emotional-expresive (T . Cretu , 2000 , p .91 ). In anumite situatii elevul ascunde ceva ce nici lui nu-i place si reuseste sa simuleze in mod convingator alte trairi. Se formeaza o zona secreta a vietii lui care este unul din semnele iesirii din copilarie.
9. ASPECTE CENTRALE ALE DEZVOLTARII
MOTIVATIEI LA SCOLARUL MIC
In ceea ce priveste evolutia motivatiei la scolarul mic sunt de mentionat doua aspecte importante: trecerea treptata de la motivatia extrinseca la cea intrinseca si amplificarea motivatiei sociale a invatarii fata de cea personala si subordonarea treptata a acesteia din urma (T. Cretu , 2000 , p .92 )
La inceput, copiii merg la scoala pentru ca asa zic parintii, au terminat cu gradinita , sunt pregatiti pentru scoala (imbracaminte si rechizite ), curiosi de ce va fi, cum va fi etc.. Daca la acestea se adauga un debut scolar bun; daca mecanismele cognitive se desfasoara in conformitate cu sarcinile de invatare, curiozitatea initiala se transforma in curiozitate epistemica - copilul doreste sa-si insuseasca noi cunostinte, sa afle raspunsul la anumite intrebari. Catre varsta de 9 ani incep sa apara preferintele pentru anumite discipline scolare si elevul constata singur la ce obiect este bun.
Tot acum invatarea scolara este motivata si de dorinta succesului, de calificative mari, admiratia colegilor si dorinta copilului de a raspunde asteptarilor parintilor si invatatoarei. In motivatia copilului este foarte importanta atitudinea invatatoarei fata de acesta; cu cat ii acorda mai multa atentie, incredere, il antreneaza si-1 valorizeaza in clasa cu atat creste implicarea copilului in actul educational. Cea de-a treia copilarie este stadiul in care elevii manifesta receptivitate fata de cerintele invatatoarei si fata de ale adultilor in general si aceste atitudini influenteaza progresele pe toate planurile. Pe langa toate acestea cresc si motivele sociale de invatare. Copilul care a obtinut un anumit loc in urma rezultatelor foarte bune simte nevoia sa si-l pastreze mentinand prin acesta admiratia celor din jur .
Scolaritatea mica este stadiul in care si interesul pentru joc este puternic . Jocul este foarte important in aceasta perioada deoarece prin el se descarca tensiunile generate de activitatea scolara. Interesul pentru joc se imbina foarte bine cu interesul pentru grup. Scolarul poate fi integrat acum in doua grupuri diferite : clasa si colegii de care se simte puternic legat si grupul de copii din preajma locuintei mai putin stabil si orientat catre joc.
De asemenea interesul pentru lectura se cristalizeaza incepand din clasa a II a. La inceput copiii prefera legendele istorice dar, treptat ei sunt atrasi de carti care au eroi si actiuni palpitante, literatura stiintifico-fantastica.
Interesul pentru natura este si el bine dezvoltat la elevii mici, interesul pentru domeniul tehnicii ( elevii mei au solicitat ore de informatica si am vazut ca le place foarte mult ), interesul pentru dans, la unii scolari mici apar unele preocupari pentru a-si alcatui colectii eterogene si de mica semnificatie, preocupari ce pot pregati cristalizarea intereselor de colectionare mai semnificative din viitor .
ASPECTE PRINCIPALE ALE DEZVOLTARII PERSONALITATII COPILULUI DE VARSTA
SCOLARA MICA
Activitatile pe care le desfasoara copilul de la intrarea in scoala sunt factorii cei mai importanti care guverneaza schimbarile semnificative in planul personalitatii acestuia. Ele structureaza dezvoltarea capacitatilor formate anterior si dau nastere altora .
Tot ce tine de interactiunea copilului cu egalii sai: dialogul, imitarea, compararea cu altul, intalnirile zilnice etc., sunt mecanisme de modelare si perfectionare continue discrete ale personalitatii si tuturor structurilor psiho-eomportamentale.
Acesti factori contribuie la consolidarea unor aptitudini, trasaturi de caracter, conduite, constiinta morala pe care copiii le au din prescolaritate, dar se formeaza si altele noi.
In ansamblul sau personalitatea copilului din acest stadiu are o anumita instabilitate si fragilitate caracteristica pentru copilarie. Sunt momente cand scolarul, mai ales in ultimele clase este dezorientat, inadaptat, ineficient si are nevoie de sprijinul adultului. In comparatie insa cu prescolarul, elevul desfasoara activitati complexe, stabileste relatii mai constiente si este capabil sa demonstreze capacitati noi de autonomie si independenta .
In ceea ce priveste aptitudinile si capacitatile micului scolar sunt in progres continuu si se vad in rezultatele copiilor.
Asa cum am mai spus in lucrarea de fata , in aceasta perioada este foarte importanta relatia cu covarsnicii care-i ofera copilului alte experiente sociale decat cele din mediul familial, ii adanceste sociabilitatea, ii dezvolta atitudini noi: respectul fata de punctul de vedere al celuilalt, colaborare si cooperare, apartenenta la grup, mandria de a apartine unei anumite scoli sau clase. Tot in cadrul grupului el se poate afirma fizic si psihic.
" El poate, in acest cadru, sa elaboreze primele relatii sociale perfect reciproce care constituie un antidot eficient pentru egocentrismul lui original ' ( P. Osterrieth , 1976 , p.149 )
Dezvoltarea caracterului ramane in continuare in baza modelelor oferite de parinti sau celor oferite de mass-media. Totusi, procesul instructiv-educativ dezvolta unele trasaturi de caracter: sarguinta, constiinciozitatea, punctualitatea, autoexigenta, etc.
Comunicarea din spatiul scolii si din grupurile informale dar si relatiile ce se stabilesc aici conduc la schimbari si in conduita morala a micului scolar despre care Piaget afirma urmatoarele : " sentimentele morale, legate la inceput de o autoritate sacra , dar care fiind exterioara, nu poate sa impuna decat o obedienta relativa, evolueaza in sensul unui respect natural si al unei reciprocitati, ale carei efecte de decentrare sunt mai profunde si mai durabile' ( J. Piaget , B. Inhelder , 1976, p.107 )
Tot acum pot aparea chiar si primele minciuni adevarate daca se exercita asupra lor o severitate exagerata din partea parintilor sau a invatatoarei.
Imaginea de sine si constiinta de sine, desi impalpabile, greu de conturat si definit joaca un rol deosebit de important in conduita, omul fie apara, fie afirma, fie tinde si doreste sa creeze celor din jur o imagine anume despre sine, de obicei favorabila. In acest stadiu se poate vorbi despre aparitia interesului pentru viata interioara proprie si amplificarea imaginii de sine in planul fizic, spiritual si social.
In ceea ce priveste Eul fizic se refera la caracteristicile de natura fizica. Copilul nu acorda mare importanta acestuia mai ales la inceputul stadiului cand trece prin fata oglinzii fugitiv. Catre sfarsitul stadiului insa, aspectul exterior incepe sa il preocupe mai mult.
Eul spiritual este implicat mai mult in invatarea scolara, elevul fiind influentat evaluarile invatatoarei, de aprecierile si admiratia copiilor. Din acest motiv, atat parintii cat si invatatoarele trebuie sa fie atente la felul in care ii valorizeaza pe copii deoarece acestea au urmari de durata si profunzime in dezvoltarea imaginii de sine a copiilor.
Eul social este considerat in lumina relatiilor cu ceilalti. Fiecare copil stie care ii. este locul in grupul clasa, isi da seama pentru ce il apreciaza sau nu colegii. Un elev cu rezultate scolare foarte bune este preferatul clasei, ales lider, este factor de identificare pentru ceilalti. Cel care intampina dificultati este de cele mai multe ori marginalizat si trebuie sa intre in atentia si sarcinile educationale ale invatatoarei . (R. Iucu , 2000 , p .161 )
Dezvoltarea imaginii de sine in cea de-a treia copilarie este incontestabil puternic influentata de adaptarea copilului la un nou mediu social si de invatare, care devine dominant in aceasta perioada.
"Atentia pe care invatatoarea trebuie sa o acorde dezvoltarii unei imagini de sine cat mai corecte la elevii sai reprezinta o conditie a reusitei scolare din acest ciclu si o latura a pregatirii pentru intrarea in urmatoarele trepte scolare si pentru integrarea generala in viata si societate ' spune T . Cretu, 2000, p . 102 si experienta la clasa m-a confirmat pe deplin acest adevar.
c. Invatarea matematici in clasele I - II
1. Obeiective
Obiectivele educationale sunt induse de idealul educational si de finalitatile sistemului de invatamant, care contureaza, intr-o etapa istorica data, profilul de personalitate dorit la absolventii sistemului de invatamant. Finalitatile sistemului se concretizeaza in finalitatile pe niveluri de scolaritate (prescolari, primar, gimnazial si liceal), care descriu specificul fiecarui nivel de scolaritate din perspectiva politicii educationale.
Finalitatile invatamantului primar sunt:
asigurarea educatiei elementare pentru toti copiii;
formarea personalitatii copilului respectand nivelul si ritmul sau de dezvoltare;
inzestrarea copilului cu acele cunostinte, capacitati si atitudini care sa stimuleze raportarea efectiva si creativa la mediul social si natural si sa permita continuarea educatiei.
Curriculum-ul national, elaborat in anul 1998, realizeaza o periodizare a scolaritatii prin gruparea mai multor niveluri de clase, care au in comun anumite obiective. Aceste cicluri curriculare au scopul de a evidentia obiectivul major al fiecarei perioade scolare si de a regala procesul de invatamant din acea perioada.
Astfel, s-a format ciclul achizitiilor fundamentale, ce cuprinde copiii de 6-8 ani, aflati in gradinita si in clasele I - II, ciclul de dezvoltare, cuprinzand copiii de 9-12 ani, corespunzator claselor II - VI si ciclul de observare si orientare, ce include copiii de 13-14 ani, din clasele a VII-a si a VIII-a.
La nivelul invatamantului primar, ciclul achizitiilor fundamentale are ca obiective majore acomodarea la cerintele sistemului scolar si alfabetizarea initiala. Acest ciclu urmareste:
asimilarea elementelor de baza ale principalelor limbaje conventionale (scris, citit, calcul);
stimularea copilului in vederea perceperii, cunoasterii si adaptarii la mediul apropiat;
formarea motivarii pentru invatare.
Ciclul de dezvoltare are ca obiectiv major formarea capacitatilor de baza necesare pentru continuarea studiilor. Acest ciclu urmareste:
dezvoltarea achizitiilor lingvistice, a competentelor de folosire a limbii romane, a limbii materne si a limbilor straine, pentru exprimarea corecta si eficienta in situatii variate de comunicare;
dezvoltarea capacitatii de a comunica, folosind diferite limbaje specializate;
dezvoltarea gandirii autonome si a responsabilitatii fata de integrarea in mediul social.
Studiul matematicii in ciclul primar urmareste ca toti elevii sa-si formeze competentele de baza vizand: numeratia, calculul aritmetic, notiuni intuitive de geometrie si masurarea marimilor.
In acest context, obiectivele cu cel mai mare grad de generalitate, numite obiective cadru, sunt:
cunoasterea si utilizarea conceptelor specifice matematicii;
dezvoltarea capacitatilor de explorare/investigare si de rezolvare a problemelor;
formarea si dezvoltarea capacitatii de a comunica utilizand limbajul matematic;
dezvoltarea interesului si a motivatiei pentru studiul si aplicarea matematicii in contexte variate.
La nivelul fiecarei clase, aceste obiective sunt detaliate si precizate prin obiectivele de referinta.
Astfel, la clasa I, primul obiectiv cadru se materializeaza in urmatorul set de obiective de referinta, exprimate in termeni de capacitati dorite la elevi:
sa inteleaga sistemul pozitional de formare a numerelor din zeci si unitati;
sa scrie, sa citeasca si sa compare numerele naturale de la 01a 100;
sa efectueze operatii de adunare si scadere in concentrul 0-30, fara trecere peste ordin;
Cel de-al doilea obiectiv cadru se regaseste in urmatoarele obiective de referinta:
sa stabileasca pozitii relative ale obiectelor in spatiu;
sa recunoasca forme plane si forme spatiale, sa sorteze si sa clasifice dupa forma, obiecte date;sa sesizeze asocierea dintre elementele a doua categorii de obiecte, desene sau numere mai mici ca 20, pe baza unor criterii date, sa continue modelele repetitive reprezentate prin obiecte, desene sau numere mai mici decat 10;sa se continue modelele repetitive reprezentate prin obiecte, desene sau numere mai mici decat 10;
sa exploreze modalitati de a descompune numere mai mici ca 30, in suma sau diferenta folosind obiecte, desene sau numere;
sa rezolve probleme care presupun o singura operatie dintre cele invatate;
sa compuna oral exercitii si probleme cu numere de la 0 la 30.
sa masoare dimensiunile, capacitatea sau masa unor obiecte folosind unitati de masura nestandard aflate la indemana elevilor;
sa recunoasca orele fixe pe ceas;
sa estimeze numarul de obiecte dintr-o multime si sa verifice prin numarare estimarea facuta;
Al treilea obiectiv cadru se reflecta in obiectivul de referinta
3.1. sa verbalizeze in mod constant modalitatile de calcul folosite in rezolvarea unor probleme practice si de calcul;
Cel de-al patrulea obiectiv cadru se regaseste in obiectivele de referinta
4.1. sa manifeste o atitudine pozitiva si disponibilitate in a utilizarea numerelor;
4.2. sa constientizeze utilitatea matematicii in viata cotidiana.
Toate aceste obiective sunt valabile pentru curriculum-ul nucleu, trunchiul comun ce corespunde numarului minim de ore din planul de invatamant.
La clasa a Il-a sunt prevazute urmatoarele noi continuturi invatarii:
numere naturale pana la 1000 (formare, scriere, citire, comparare, ordonare);
adunarea si scaderea numerelor naturale in concentrul 0-100, fara si cu trecere peste ordin; inmultirea numerelor naturale in concentrul 0-50; impartirea dedusa din tabla inmultirii (se transfera in clasa a IH-a incepand cu anul scolar 2004-2005);
elemente intuitive de geometrie: punct, segment, linie dreapta, linie franta, linie curba; interiorul si exteriorul unei figuri geometrice; exercitii de observare a obiectelor cu forma de paralelipiped dreptunghic;
masurarea marimilor si unitatilor de masura pentru lungime (metrul), capacitate (litrul), masa (kilogramul), timp (minutul); monede; utilizarea instrumentelor de masura adecvate: metrul, rigla gradata, cantarul, balanta.
2. Continuturi
Curriculum-ul nucleu prevede urmatoarele continuturi ale invatarii la clasa I:
elemente pregatitoare pentru intelegerea conceptului de numar natural;
numere naturale de la 0 la 100: citire, scriere, comparare, adunare;
adunarea si scaderea numerelor naturale in concentrul 0-30, fara trecere peste ordin;
figuri geometrice: triunghi, dreptunghi, patrat, cerc;
masurari cu unitati nestandard pentru lungime, capacitate, masa; masurarea timpului (unitati de masura: ora, ziua, saptamana, luna; recunoasterea orelor fixe pe ceas).
Clasa a IlI-a are urmatoarele noi continuturi ale invatarii:
numere naturale pana la 1000000;
adunarea si scaderea numerelor naturale in concentrul 0-1000; inmultirea numerelor naturale in concentrul 0-100; impartirea (inclusiv cea cu rest) in acelasi concentru; ordinea efectuarii operatiilor si folosirea parantezelor rotunde;
elemente intuitive de geometrie: poligon; exercitii de observare a obiectelor cu forme de cilindru sau de con;
masurarea marimilor si a unitatilor de masura pentru lungime (multiplii si submultiplii metrului), capacitate (multiplii si submultiplii litrului),masa (multiplii si submultiplii kilogramului), timp (anual), menede si bancnote.
In clasa a IV-a sunt urmatoarele noi continuturi ale invatarii:
numere naturale: clase(unitati, mii, milioane, miliarde);caracteristicile sistemului de numeratie folosit (zecimal si pozitional); scrierea cu cifere romane;
adunarea si scaderea numerelor naturale fara si cu trecere peste ordin; inmultirea cand un factor are cel mult doua cifre sau este 10, 100, 100; impartirea la un numar de o cifra (diferenta de 0) sau la 10, 100, 1000 (a numerelor a caror scriere se termina cu cel putin unul, doua sau trei zerouri); ordinea efectuarii operatilor si folosirea parantezelor;
fractii: notiunea de fractie; fractii egale, reprezentari prin desene; fractii echiunitare, supraunitare; compararea fractiilor; adunarea si scaderea fractiilor cu acelasi numitor; aflarea unei fractii dintr-un intreg;
elemente intuitive de geometrie: unghi, drepte paralele; rombul; perimetrul (dreptunghiului si patratului); aria;
masurarea marimilor si unitati de masura, cu transformari ale multiplilor si submultiplilor unitatilor principale pentru lungime, capacitate, masa; unitati de masura pentru timp (deceniul, secolul, mileniul); monede si bancnote.
3. Strategii didactice
II a. Rezolvarea problemelor de matematica in clasele I-II
Valentele formative ale activitatii de rezolvare a problemelor tip
In general prin problema tipica se intelege acea constructie matematica a carei rezolvare se realizeaza pe baza unui algoritm specific. O astfel de problema este cosiderata teoretic rezolvata in momentul in care i-am stabilit tipul si suntem in posesia algoritmului de rezolvare. Pentru a identifica metoda (algoritmul) am sa rezolv ca model una dintre cele mai semnificative probleme apartinand unui anumil tip, iar pentru unele dintre ele voi realiza si o discutie introductiva adecvata nivelului intelegere si de cunoastere a elevului.
Am sa ma opresc astfel asupra problemelor care se rezolva prin metoda figurativa, metoda falsei ipoteze, metoda retrograda, metoda reducerii la acel termen de comparatie.
a) Plecand de la definitia problemelor tipice, problemele care se rezolva prin metoda figurativa nu le putem include strict in categoria celor tipice deoarece putem sa gasim un algoritm de rezolvare aplicabil tuturor problemelor de acelasi fel. Putem descrie insa in ce consta metoda figurativa. Deseori cel care rezolva problemele de matematica (si nu numai) simte nevoia sa-si aproprie datele problemei, precun relatiile dintre acestea si textul enuntului. Pentru aceasta se realizeaza un desen, o figura, un model care sa oglindeasca ceea ce am aratat mai sus.
Problemele care se rezolva prin metoda figurativa pot fi impartite in doua categorii:
Cu date sau marimi
'discrete', intelegand prin aceasta ca marimile pot fi
numarate cate una si ca se pot pune in corespondenta
dupa anumite categorii
(criterii).
In acest caz marimile le figuram prin simboluri.
Cu date sau marimi 'continue', caz in
care le figuram prin segmente.
Exemplul nr.l :
'Suma dintre un numar natural, jumatatea sa si dublul sau este 140. Sa se determine numarul.'
Reprezentand printr-un segment jumatatea numarului avem :
jumatatea numarului | |
numarul |----- ----- ----- | -----
dublul numarului |----- ----- ----- | -----
Din aceasta reprezentare putem afla jumatatea numarului
Daca 20 este jumatatea numarului, inseamna ca numarul cautat este 20 x 2=40
Exemplul nr. 2 :
'Intr-o gospodarie sunt rate si oi. In total sunt 40 de capete si 100 de picioare. Cate rate si cate oi sunt ?'
Pornind de la faptul ca ratele au 2 picioare, iar oile au 4 picioare reprezentam prin ovale aceste vietati. Ceea ce este foarte sigur este faptul ca si ratele si oile au cel putin 2 picioare.


Gasim astfel numarul de oi oi. Restul de vietati ramase sunt rate.
Raspuns in curte erau oi si rate
Se va realiza proba : 10x4 30x2 = 100 picioare oi rate
b) In continuare ma voi referi la probleme de aflare a doua numere cunoscand suma sau diferenta lor si raportul lor.
Exemplu
'Intr-un cos sunt cu mere mai mult decat in alt cos. Daca de mere trecute din primul cos in al doilea, in acesta vor fi de ori mai multe ca in primul. Cate mere erau in fiecare cos?'
Luam din primul cos mere, ceea ce inseamna ca am luat cele mere si mere. Unde le punem? Le punem in al doilea cos care va avea mai multe mere decat primul cu
Sa reprezentam grafic
![]()
22 + 46 = 68
Luam acum 46 mere din primul cos adica 24 si 22, si le punem in al doilea cos.
Acum in al doilea cos sunt de 3 ori mai multe decat in primul. Care este noua diferenta ? Din grafic rezulta ca aceasta este de :
46 + 22= 68 mere.
Reformulam problema :'Intr-un cos sunt de 3 ori mai multe mere decat in al doilea cos. Iar in al doilea cos sunt cu 68 mere mai multe decat in primul. Cate mere sunt in fiecare cos?'
Dupa aceasta reformulare cunoastem diferenta :
D = 68 si raportul lor R = 3
D 68 68 .
34 mere
R-l 3-1
Numarul merelor din al doilea cos, fiind de 3 ori mai mare, este :
3x34 = 102 (mere). Revenim la enuntul initial:
34 + 46 = 80 (mere in primul cos)
= 56 (mere) sau 102 - 46 = 56 (mere in al II-lea cos).
c) Probleme de egalare a
datelor. Metoda comparatiei.
Exemplu:
8 baieti si 14 fete au recoltat 620 kg de morcovi, iar alta data 8 baieti si 4 au recoltat 320 kg. Cate kg de morcovi a recoltat in medie pe zi o fata si cate kg un baiat?
8 baieti ______ 14 fete ________ 620 kg
8 baieti ______ 4 fete ________ 320 kg
Scazand membru cu membru obtinem :
0 baieti _______ 10 fete _______300 kg
=> 0 baieti _______ 1 fata ______ 300 : 10 = 30 kg
8 baieti _______ 4 fete ______ 320 kg
Cum 4 fete recolteaza 4 x30 = 120 kg iar 8 baieti si 4 fete recolteaza 320 rezulta ca 8 baieti recolteaza :
320 kg-120 kg = 200 kg.
Deci 1 baiat recolteaza
200 :8 = 25 kg morcovi.
d) Probleme care se rezolva prin metoda falsei ipoteze.
Problemele din aceasta categorie sunt foarte numeroase, putand afirma ca orice probleme ale carei date sunt marimi proportionale poate fi rezolvata prin me falsei ipoteze. La ce se refera? Se pleaca de obicei de la intrebarea probleme sensul ca asupra marimii ce o cautam facem o presupunere complet arbitrara aceasta situatie refacem problema pe baza presupunerii facute ajungand la un rezultat care nu concorda cu cel real; este fíe mai mare, fíe mai mic decat acesta.
Exemplu
'Un biciclist urca cu km pe ora si coboara aceasi panta cu km pe ora. Stiind ca drumul urcat si coborat a durat ore si minute, sa se afle lungimea drumului
Am observat ca marimile care intervin, si anume distanta si timpul, sunt proportionale, si atentia se indreapta spre intrebarea problemei. Asadar, presupun ca lungimea drumului ar fi de km Refacem problema. Cunoastem lungimea drumului si vitezele cu care urca si coboara panta, putem afla in cat timp a urcat, apoi in cat timp o coboara, si, in fine timpul total la urcare si coborare.
Comparam cu cel real din problema, adica ore si minute, si aflam raportul dintre marimea propusa si cea reala. Numarul pe care l-am gasit este 'coeficientul corectie' care ne va permite modificarea presupunerii facute.
Aflam timpul de urcare algoritm : 60 : 6 = 10 ore (fals)
Aflam timpul de coborare ore (fals)
Aflam timpul total ore (fals)
Comparam rezultatul presupunerii, adica ore cu cel real, adica h si 15 min.:
13 4
13x
15 3
3x
60
si vedem ca este mai mare decat cel real
Acesta este 'coeficientul de corectie'. Va trebui sa corectam presupunerea facuta, in sensul micsorarii ei de ori.
Aflam lungimea totala a drumului
km
R: km
e) Probleme care se rezolva folosind metoda mersului invers Exemplu
'Un biciclist merge in prima ora cu km mai putin decat jumatate din drumul pe care-l avea de parcurs; ora a doua merge din drumul ramas si inca 1 km, dupa care mai are de parcurs km Ce lungime are drumul
Reprezentam grafic
I ora |----- ----- ----------------
----|------| R1
1 3 km
R2
Aflam a cata parte din Rl reprezinta R2 :
R2 + 1 km = 2/5 din Rl
km + 1 km = 4 km
km : 2 = 2 km - 1/5 din Rl
Aflam Rl :
2kmx7 14km
Aflam cat reprezinta jumatate din lungimea drumului:
14 km -1 km=13 km .
Aflam lungimea drumului:
13x2 = 26 km.
Conceptul de problema
' A rezolva o problema inseamna a gasi o iesire dintr-o dificultate, inseamna a gasi o cale de a ocoli un obstacol, de a atinge un obiectiv care nu este direct accesibil. A gasi solutia unei probleme este o performanta specifica inteligentei, iar inteligenta apanajul specific speciei umane; se poate spune ca, dintre toate indeletnicirile omenesti cea de rezolvare a problemelor este cea mai caracteristica ' .
G. Polya - 'Descoperirea in matematica. Euristica rezolvarii problemelor ' -Editura Stiintifica Bucuresti 1971 pag.37
Notiunea de problema are un continut larg, cuprinzand o gama variata preocupari si actiuni, in domenii foarte diferite .
In general orice chestiune de natura practica sau teoretica ce reclama o rezolvare, o solutionare, poarta numele de problema.
Avand in vedere ca orice proces de gandire este declansat de o intrebare pe care si-o pune sau care i se pune omului, se admite ca formularea unui raspuns clar si precis la o astfel de intrebare constituie o problema.
Referitor la matematica, prin problema se intelege orice chestiune a carei solutionare se poate obtine prin procese de gandire si calcul.
Valoarea formativa a rezolvarilor de probleme sporeste pentru ca participare mobilizarea intelectuala a elevilor la o astfel de activitate este superioara altor demersuri matenatice, elevii fiind pusi in situatia de a descoperi si insusi modalitatile de rezolvare si solutionare, sa formuleze ipoteze si apoi sa le verifice, sa faca asociatii de idei si corelatii inedite.
Activitatea gandirii se manifesta cu precadere in rezolvarea de probleme. O problema de gandire apare atunci cand in calea activitatii practice sau teoretice apare un obstacol. Atunci cand nu exista un astfel de obstacol si situatia poate fi rezolvata pe baza deprinderilor anterioare formate si a unor solutii existente in experienta castigata, atunci gandirea nu mai este confruntata cu o noua problemaa, deci nu exista o problema rezolvat.
Procesul de gandire se declanseaza ori de cate ori nu putem face fata unor situatii problema numai prin mijloacele invatate.
Rezolvarea de probleme pune la incercare in cel mai inalt grad capacitatile intelectuale ale elevilor le solicita acestora toate disponibilitatile psihice, in special inteligenta, motiv pentru care matematicii i se acorda o foarte mare atentie.
Viata constituie un permanent furnizor de probleme, intrucat in activitatea practica si teoretica a omului se ivesc in mod frecvent probleme din cele mai variate, ce se cer rezolvate.
In activitatea teoretica si practica omul intalneste atat situatii identice in a caror rezolvare aplica metode si procedee standardizate de tip algoritmic, dar si situatii noi pentru care nu gaseste solutii in experienta dobandita sau intre mijloacele deja invatate. In cazul situatiilor-problema este nevoie de explorarea situatiei prin aplicarea creatoare a cunostintelor si tehnicilor de care dispune cel ce urmeaza sa rezolve problema , scopul fiind acela al descoperirii implicatiei ascunse a necunoscutei, a elaborarii rationale a solutiei.
La matematica elevii percep o problema ca o situatie in care trebuie sa intervina rationamentul sistematic.
Cu cat problema este mai complexa, cu atat acest rationament se cere a fi dezvoltat si necesita o severa ordonare a scrierii de intrebari si raspunsuri cuprins enunt pentru a se ajunge la solutia problemei.
Problema de aritmetica reprezinta transpunerea unei situatii practice in relatii matematice, in care, pe baza valorilor numerice date ce se gasesc intr-o anumita dependenta unele fata de altele si toate fata de valoarea numerica necunoscuta, se cere sa determine aceasta necunoscuta.
Exemplu: Suma dintre un numar natural, jumatatea sa si sfertul sau este 77. Sa se determine numarul.
Orice problema matematica trebuie sa contina o necunoscuta, ceva care este cunoscut, este dat (datele problemei ) si existenta unei conditii care arata in ce fel de necunoscuta este legata de date, conditia fiind partea esentiala a problemei.
In rezolvarea unei probleme este necesar sa intelegem continutul problemei: delimitam, din capul locului, ceea ce stim si ceea ce nu stim, pe baza textului problemei ( a datelor si a conditiei ), precum si directia in care trebuie sa se desfasoare gandirea pentru a ajunge sa se raspunda la intrebarea problemei.
Sunt si cazuri cand textul problemei ajuta mai putin orientarea, organizarea rationamentului in directia necesare, probleme cu relatii mai putin evidente, ba chia relatii ascunse, care obliga la o selectare a datelor dupa 'functia ' lor in problema. Aceasta necesita o anliza mai profunda, solicitand participarea mai activa a gandirii.
In general, intre exercitiu si problema distinctia se face in functie de prezenta sau absenta textului prin care se dau date si corelatii intre ele si se cere, pe baza acestora gasirea unei necunoscute.
Exercitiul ofera elevului datele (numerele cu care se opereaza si semnele operatiilor respective), sarcina lui constand in efectuarea calculelor dupa tehnici si metode cunoscute. Problema impune in rezolvarea ei si o activitate de descoperire.
Exemplu : 'Suma a trei numere consecutive este 213 . Sa se determine cele trei numere'.
Matematic vorbind, distinctia dintre exercitiu si problema trebuie facuta dupa forma exterioara a acestora si dupa natura rezolvarii. Clasificarea unor enunturi matematice in exercitii si a altora in probleme nu se poate face insa in mod transant fara a tine seama si de experienta de care dispune si pe care o poate utiliza cel care o rezolva. Un enunt poate fi o problema pentru un copil din clasa I, un exercitiu pentru cel clasa a IV a si doar ceva foarte cunoscut pentru un matematician.
Pe parcurs, cand elevul isi insuseste modalitati de rezolvare mai generale si mai unitare, pe masura ce creste experienta lui in rezolvarea problemelor, treptat, enunturi care constituiau pentru el probleme, devin simple exercitii.
Efortul pe care il face elevul in rezolvarea constienta a unei probleme presupune o mare mobilizare a proceselor psihice de cunoastere volitive si, firesc , motivational afective.
Dintre procesele cognitive, cea mai solicitata si antrenanta este gandirea, operatiile logice de analiza, sinteza, comparatie, abstractizare si generalizare. Rezolvand problemele, formam la elevi priceperi si deprinderi de a analiza situatia data de problema, de a intui si descoperi calea prin care se obtine ceea ce se cere in problema. In acest mod, rezolvarea problemelor contribuie la cultivarea si dezvoltarea capacitatilor creatoare ale gandirii, la sporirea flexibilitatii ei, a capacitatilor anticipativ-imaginative, la educarea perspicacitatii si spiritului de initiativa, la dezvoltarea increderii in fortele proprii.
Rezolvarea problemelor de matematica contribuie la clarificarea, aprofundari fixarea cunostintelor invatate la acest obiect de studiu. In acelasi timp, explicarea multora dintre problemele teoretice se face prin rezolvarea uneia sau mai multor probleme in cadrul carora se subliniaza o proprietate, definitie sau regula ce urmeaza a fi invatata .
Prin rezolvarea problemelor de matematica elevii isi formeaza deprinderi eficiente de munca intelectuala, care se vor reflecta pozitiv si in studiul altor disciplina invatamant isi cultiva si educa calitatile moral volitive. Activitatile matematice de rezolvare si compunere a problemelor contribuie la imbogatirea orizontului de cultura generala a elevilor prin utilizarea in continutul problemelor a unor cunostiinte pe care le studiaza la alte discipline de invatamant. Este cazul informatiilor legate de distanta, viteza, timp, pret, plan de productie, norma de productie, cantitate, dimensiune, masa, arie etc. Problemele de aritmetica, fiind strans legate cel mai adesea prin insasi enuntul lor de viata, de practica, genereaza la elevi un simt al realitatii de tip matematic, formandu-le deprinderea de a rezolva si alte probleme practice pe care viata le pune in fata lor. Rezolvarea sistematica a problemelor de orice tip sau gen are drept efect formarea la elevi a unor seturi de priceperi, deprinderi si atitudini pozitive care le posibilitatea de a rezolva in mod independent probleme, de a compune ei insisi probleme.
Exemplu : Alcatuiti o problema a carei rezolvare sa se scrie : 1000-250 : 5 =
In rezolvarea problemelor intervin o serie de tehnici si procedee, moduri de actiune, deprinderi si abilitati de munca intelectuala. Astfel, sunt necesare unele deprinderi si abilitati cu caracter general cum sunt: orientarea activitatii mintale asupra datelor problemelor, punerea in legatura logica a datelor, capacitatea de a izola cee este necunoscut, extragerea acelor cunostinte care ar putea servi la rezolvarea problemei precum si unele deprinderi specifice referitoare la detaliile actiunii cum sunt cele de genul deprinderilor de calcul.
Exemplu :
Aflati;
produsul dintre numerele: 346 - 340 si 72 : 9;
suma dintre numarul 121 si produsul numerelor 5 si 9 ;
diferenta dintre numarul 147 si produsul numerelor 5 si 9.
In cautarea solutiei, gandirea trebuie lasata libera sa iscodeasca, sa incerce chiar daca porneste pe drumul fara sansa de reusita .
Exemplu :
' Pentru infrumusetarea clasei elevii au adus ghivece cu flori . Daca ar mai fi 2 ghivece ar fi fost 10.
Cate ghivece cu flori au adus elevii ? ' .
Actiunea infrigurata a cautarii are o eficienta formativa mult mai bogata decat dirijarea elevului catre solutie, care-l scuteste de efort si de trairea emotiilor cautarii bucuriei descoperirii.
Rezultatele obtinute de elevi in activitatea de rezolvare de probleme nu sunt consecinta numai a dotarii intelectuale, ci si a muncii sustinute, a pasiunii depuse experientei anterioare in acest domeniu .
Ele sunt dependente de gradul de complexitate a cunostintelor si deprinde intelectuale, si in esenta de metodele de predare, de maiestria invatatorului.
Astfel, prin continutul lor, prin tehnica de predare si solutionare utilizate, rezolvarea problemelor de matematica conduce la formarea patriotismului elevilor, la cultivarea si educarea unei noi atitudini fata de munca, a spiritului de colectivitate prieteniei, a disciplinei constiente, dar si a spiritului emulativ, a competitiei cu sine si cu ceilalti. Nu pot fi uitate nici efectele benefice pe planul valorilor auto-educative, al conduitei rezolutive .
3. Metodologia rezolvarii problemelor compuse
Tinand cont de faptul ca gandirea copilului este concreta, legata de imaginile lucrurilor, ca el poate urmari procesele de gandire numai daca lucreaza efectiv obiectele specifice in problema sau in reprezentarea acestora, primele probleme care se rezolva trebuie sa fie probleme formulate pe baza actiunilor ce se petrec in mod real in fata elevilor, a caror autenticitate mintea elevului nu o pune la indoiala, trecand treptat la actiuni bazate pe reprezentari, adica la actiuni veridice, pe care elevii pot sa si le imagineze pe baza unor procese anterioare de perceptie .
Pentru elevii claselor I-IV pornirea de la realitatea cunoscuta si traita de acestia pentru descoperirea notiunilor si a regulilor, cu aplicarea acestora in diferite domenii de activitate, constituie conditia fundamentala a actului invatarii.
Incepand cu clasa I elevul se familiarizeaza cu expresii ca: 'problema', ' datele problemei ' , ' rezolvare ', specifice limbajului matematic, de asemenea este pus in situatii deosebite de rezolvare a unor probleme simple (la inceput) si apoi a problemelor compuse. Cu aceasta categorie de probleme ma voi ocupa in detaliu in cele ce urmeaza.
Pentru a introduce primele probleme compuse, adica pentru a realiza trecere la probleme simple la cele compuse exista doua posibilitati:
realizarea unei actiuni care sa cuprinda doua faze distincte: formularea problemei si apoi rezolvarea acelei probleme;
rezolvarea succesiva a doua probleme astfel formulate incat rezultatul primei probleme sa constituie un element al celei de a doua .
Pentru intelegerea acestui fenomen am folosit probleme in actiune, ca de exemplu:
' Maria are 5 trandafiri. Sora ei ii mai da 3 trandafiri . Cati trandafiri are Maria ? '
Am regizat problema iar copiii au inteles ce s-a intamplat. Le-am cerut apoi spuna cati trandafiri are Maria ( 8 trandafiri). Intrebandu-i ' De ce ? ' au raspuns :
' Pentru ca 5 + 3 = 8 ' obligandu-i astfel sa justifice folosirea adunarii.
Apoi am continuat:
' Mariei i se usuca un trandafir. Cati trandafiri i-au mai ramas ?
' Socotim cati trandafiri i-au mai ramas Mariei justificand folosirea operatiei 8-1=7.
Pe tabla se afla scrise cele doua probleme simple :
5 trandafiri 3 trandafiri ?
5 trandafiri + 3 trandafiri 8 trandafiri
8 trandafiri 1 trandafir ?
8 trandafiri -1 trandafir = 7 trandafiri
Elevii au recunoscut problemele si legatura dintre aceste doua probleme simple, cea de-a doua fiind continuarea celei dintai.
Cu ajutorul elevilor s-au facut formulari.
S-a prezentat continutul noii probleme :
' Maria are 5 trandafiri. Sora ei ii da 3 trandafiri. Din acestia se usuca 1 trandafir.
Cati trandafiri i-au mai ramas ? '
5 trandafiri 3 trandafiri1 trandafir ?
1) 5 trandafiri + 3 trandafiri 8 trandafiri
2) 8 trandafiri -1 trandafir = 7 trandafiri
Schema:
5 trandafiri 3 trandafiri 1trandafir ?
![]()
![]() 8 prima actinue
8 prima actinue
7 a doua actiune
Dupa rezolvarea separata a celor doua probleme simple si apoi a celei compuse se scoate in evidenta faptul ca pentru rezolvarea primelor doua probleme a fost necesara cate o operatie pentru fiecare, iar pentru cea de-a doua au fost necesare doua operatii.
Deci unele probleme se rezolva prin cate o singura operatie, iar altele prin doua operatii.
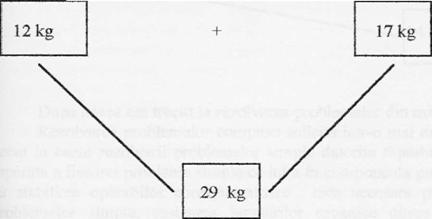
In orele urmatoare am rezolvat tot probleme de actiune .
' La un magazin s-au adus 12 kg de banane si alta data 17 kg de banane . Cate kg de banane s-au adus in total ?
=29 kg
12kg 17kg = 29kg
2) Din toate bananele s-au vandut 15 kg .
Cate kg au mai ramas ?
Copiii observa ca 29 kg care este rezultatul primei probleme se afla ca data in a doua problema.
Din cele doua probleme simple, se compune o singura problema.
' La un magazin s-au adus prima data 12 kg de banane si alta data 17 kg. Din toata cantitatea s-au vandut 15 kg .
Cate kg de banane au ramas ? '
Putem gasi dintr-o data cate kg de banane au ramas (Nu putem .De ce
(Pentru ca nu cunoastem cate kg de banane s-au adus in total !). Ce trebuie sa facem la inceput? (Sa aflam cate kg de banane s-au adus !) Ce trebuie sa facem pentru aceasta (Sa adaugam la 12 kg inca 17 kg). '

II. Cate kg de banane au ramas?
12 kg + 17 kg = 29 kg
Selectam datele din continutul problemei si facem legatura dintre aceste date .
Dupa aceea am trecut la rezolvarea problemelor din manual.
Rezolvarea problemelor compuse solicita intr-o mai mare masura gandirea logica decat in cazul rezolvarii problemelor simple datorita faptului ca, pe langa examinarea separata a fiecarei probleme simple ce intra in componenta problemei compuse, respectiv cu stabilirea operatiilor corespunzatoare, este necesara punerea in corespondenta problemelor simple, sesizarea legaturilor organice dintre ele, a dependentei reciproce, astfel incat sa se poata stabili succesiunea acestor probleme in vederea obtinerii rezultatului final.
De aceea rezolvarea unei probleme compuse trebuie sa treaca prin urmatorele etape:
intelegerea corelatiilor dintre datele problemei;
analiza logica a problemei (proiectul problemei);
algoritmul problemei; stabilirea
planului de rezolvare; stabilirea operatiilor,
scrierea si efectuarea lor;
verificarea solutiei;
alte rezolvari ale problemei (aprecierea celei mai bune;
asezarea sub forma de exercitiu;
compuneri de probleme dupa aceiasi exercitiu;
generalizarea rezolvarii problemei.
Analizarea problemei se face prin doua metode principale :
A. Metoda analitica ce inseamna a porni de la intrebarea problemei, a stabili datele in general necunoscute cu ajutorul carora se poate formula problema simpla a carei intrebare sa coincida cu intrebarea problemei date, deci pornind de la ( necunoscut la cunoscut).
Aceasta metoda este mai dificila, solicita gandirea elevilor intr-un grad mai mare avand in vedere faptul ca problema trebuie privita in ansamblul ei.
Se foloseste la clasele mari (a-III-a, a-IV-a).
B. Metoda sintetica, care inseamna a orienta atentia elevilor asupra a doua din datele problemei compuse si a formula cu aceasta o problema simpla al carei rezultat sa constituie un element al unei noi probleme simple si asa mai departe pana se ajunge la ultima problema simpla a carei intrebare coincide cu intrebarea problemei compuse date.
Rationamentul prin aceasta metoda se elaboreaza inductiv, pe baza unor sinteze succesive.
Este una din metodele mai usoare pentru elevi, accesibila acestora, dar in acelasi timp poate duce si la erori datorita faptului ca uneori in cadrul unei probleme compuse pot formula si probleme simple ce nu converg spre rezultatul final si care abat atentia gandirea elevilor pe cai laturalnice .
De aceea , este necesar ca in formularea fiecarei probleme simple sa ne punem intrebarea: Este necesar sa aflam aceasta ?
Baza dezvoltarii gandirii matematice, cu ajutorul rezolvarii si a compunerii de probleme de catre elevi, incepem sa o formam din clasa I-a, odata cu predarea operatiilor pe cale orala.
Pentru deprinderea elevilor cu modul cum trebuie gandita o problema, analizata, in vederea rezolvarii, am folosit o serie de procedee pe langa cele aratate pana acum.
Dintre acestea mentionam:
verificarea rezultatului obtinut;
completarea de catre elevi a datelor care lipsesc dintr-o problema astfel incat sa se poata rezolva, apoi rezolvarea ei.
Exemplul numarul 1.
' Intr-o livada s-au plantat 50 de pomi fructiferi. Meri_______, peri_______, iar restul piersici. Cati piersici s-au plantat ? '
Exemplul numarul 2.
' Ionel are de rezolvat _____ probleme. Intr-o zi el a rezolvat 20 de probleme, iar in alta zi 16 probleme .
Cate probleme mai are de rezolvat ? '
formularea de probleme asemanatoare;
completarea intrebarii problemei de catre elevi, apoi rezolvarea ei.
' La o cantina s-au adus o data 36 de litri de ulei si alta data 23 de litri. Tot uleiul s-a pus intr-un vas, apoi s-au consumat 17 litri pentru gatit.'
transformari de probleme simple in probleme compuse si invers ;
schimbarea unor relatii dintre datele problemei rezolvate, solicitand rezolvarea 'noii ' probleme si compararea rezultatelor;
scrierea rezolvarii cu ajutorul formulelor numerice si literale;
rezolvarea de probleme pe mai multe cai;
rezolvarea de probleme dupa datele desenate (schitate);
compuneri de probleme prin diferite procedee.
In clasa I-a modalitatile de baza in rezolvarea problemelor au constat in :
rezolvarea problemelor sistematizate pe categorii in raport cu dificultatile pe care le ridica;
analiza minutioasa a problemei pentru o buna cunoastere a datelor conditiei si a intrebarii problemei;
stabilirea legaturilor logice intre perechile respective de date si redarea printr-o schema grafica.
Exemplu:
58 baieti ..cu 27 mai putin fete ..?elevi

Dupa rezolvarea problemelor s-a realizat scrierea caii de rezolvarea prin singur exercitiu (formula numerica).
In alte cazuri schema grafica cuprinde in interiorul ei operatiile aritmetice prin care se rezolva problema.
' La o alimentara erau 2 butoaie cu ulei, primul cu 43 litri, al doilea cu 35 litri. Din primul s-au vandut 21 litri, iar din al doilea 20 litri. Cati litri de ulei mai sunt in doua butoaie?'
43..35l..21 l.20 l.?
43+35=78 21+20=41
78-41=37
43..35 l21 l20 l ?
43-21=22 35-20=15
22+15=37
(43-21)+(35-20)=37
Alcatuirea si rezolvarea problemelor dupa formule :
Exemplul 1 : a + (a - b)
'Un copil are 756 lei, iar fratele lui are cu lei mai putin Cati lei au impreuna
Exemplul (a +b (c +d sau (a -c (b -d
Nr.
Completati
intrebarea problemei pentru a avea o problema simpla si rezolvati-o
' Intr-un dulap sunt pe un raft de carti, iar pe al doilea sunt cu carti mai putin
Transformati problema simpla in problema compusa si rezolvati' scrieti intrebarea problemei
Scrieti formula numerica
Scrieti formula literala.
Modificati relatiile dintre datele problemei in asa fel incat sa se rezolve acelasi fel de operatii
Nr.
Intr-o lada sunt kg de mere iar in alta sunt cu kg mai putin
Transformati problema simpla in problema compusa si rezolvati-o screti si intrebarea problemei
Scrieti formula numerica
Scrieti formula literala
Modificati relatiile
dintre datele problemei in asa fel incat sa se
rezolve
acelasi fel de operatii
Obiectivul lucrarii a fost de a sti cu exactitate modul in care a evoluat dezvoltarea gandirii elevilor
Cunoscand aspectul acesta in clasa urmatoare am stiut pe ce anume trebuie accentul
Astfel, in clasa a doua am continuat cu rezolvarea problemelor pe baza celor doua operatii invatate, in scopul consolidarii lor. S-au rezolvat si probleme cu continut geometric (aflarea lungimii latimii, perimetrului
Odata cu invatarea urmatoarelor operatii de inmultire si impartire, am rezolvat probleme cu ajutorul acestora
Am insistat asupra rezolvarii problemelor folosind planul de rezolvare, sechema; am continuat cu extragerea formulei numerice, si in mod deosebit cu rezolvarea problemelor prin mai multe procedee
O deosebita importanta am acordat acelor probleme care adaugau o dificultate in plus, prin aceea ca ordinea datelor din problema nu coincidea cu alcatuirea perechilelor de valori
Elevii au fost pusi in situatia sa caute perechi de date care ofereau relatii matematice certe, observand ca o problema se poate rezolva prin mai multe procedee.
' Un magazin a vandut 97 de costume in 3 zile. In prima zi s-au vandut 34 costume, in a doua zi 45 costume . Cate costume s-au vandut in a treia zi ? '
Formula de rezolvare succesiva a problemei este:
a - b - c = d
Elevii au fost condusi cu ajutorul exemplelor practice, cunoscute de ei, rezolvarea logica a problemei si realizarea unei alte formule.
a-(b c) d
Totodata pornind de la relatia :
T =I + II + III
am desprins : III = T - (I + II)
Completand cu datele problemei:
III = 97-(34+
III = 18
Am reformulat apoi problema considerand necunoscuta :
'numarul de
costume vandute a doua zi' :
97 = 34 + x+ 18 => x =
x = 45
'numarul de
costume vandute in prima zi ' :
97 = x + => x =
x = 34
In continuare elevii au fost pusi in situatia sa mai rezolve astfel de probleme intrebari diferite, utilizand relatiile respective.
Specific clasei a doua a fost si deducerea principiului de rezolvare a problemei direct din datele ei in momentul analizei.
Exemplu :
'Cate portocale a mancat un copil in 3 zile, daca in prima zi a mancat 12 portocale, in a doua zi cu 4 portocale mai putin decat in prima zi, iar in a treia zi a mancat 9 portocale.'
I II III
12 portocale 4 portocale 9 portocale ?
12 portocale 12-8 portocale 9 portocale ?
Forma literala :a (a-b) c
In continuare am schimbat relatiile dintre datele problemei formuland textul astfel:
'Cate portocale a mancat un copil in trei zile, daca in prima zi a mancat 12 portocale, iar in a doua zi cu patru portocale mai mult ca in prima zi, iar in a treia mancat cu 9 portocale mai putin decat in a doua zi. '
Analizand datele a reiesit
I
II
III
12 portocale
4 portocale
9 portocale ?
12 portocale
12+4 portocale
12+4-9 portocale
portocale
12 portocale
portocale
(12+4)portocale
7portocale (12+4-9)portocale
12 portocale +16 portocale +7 portocale -35 portocale
Dupa invatarea inmultirii si impartirii, elevi au folosit aceste operatii mai intai si probleme simple de forma:
axb= c a : b = c
dupa care s-a trecut la probleme compuse ce solicitau in rezolvare operatii aritmetice combinate:
Exemplu:
'Intr-o livada sunt 72 de peri si de 8 ori mai putini meri. Cati pomi sunt in acea livada ?
Dupa parcurgerea etapelor de inceput folosite in rezolvarea unei probleme compuse, am ajuns la analiza problemei intrebuintand metoda analitico-sintetica, intrebarea ducand cu usurinta spre datele necesare.
Rezolvarea deductiva a problemei constituie exercitiu de gandire matematica pregateste terenul pentru transcrierea formulei numerice de rezolvare a problemei : formula literala.
Dupa analiza problemei am realizat scheme :
72 + ? = a doua actiune
72:8=prima actiune
72 peri ____ de 8 ori mai putini meri ? pomi
A urmat apoi realizarea formulei literale:
a = numar de peri
n = numar care arata de cate ori sunt mai putini meri
b = numar de meri
c = numar de pomi
a (a:n) a b c
In clasa a doua am intalnit si probleme a caror rezolvare este evidenta.
Exemplul nr. 1 :
' S-au cumparat 2 caiete a 200 lei caietul si 3 creioane a 100 lei bucata.
Cati lei au costat cumparaturile ? '
Elevii au dobandit capacitatea de a 'vedea' problema in intregime: au rezolvat-o sub forma de exercitiu, fiind propriu zis un exercitiu.
2 x 200 + 3 x 100
Exemplul nr. 2 :
'Pentru efectuarea unor reparatii, la un santier s-au trimis intr-o zi 4 echipe a 10 muncitori, iar a doua zi 18 muncitori. Cati muncitori s-au trimis in cele doua zile ? '
4x10
In clasa a IlI-a am continuat cu rezolvarea problemelor cu doua operatii, la care am adaugat planul scris (sub forma de intrebari, apoi concis).
Exemplu :
' Intr-o tabara au venit in prima serie 208 elevi, iar in a doua serie cu 25 elevi mai multi. Cati elevi au fost in total in tabara ?'
S-a alcatuit urmatorul plan de rezolvare :
Cati elevi au fost in a doua serie ? 1. Elevi in a doua serie.
Cati elevi au fost in total ? 2. Totalul elevilor.
Dupa formarea la elevi a deprinderilor de realizare a planului scris in rezolvarea problemelor prin doua operati, s-a trecut la rezolvarea problemelor prin trei operatii.
Am continuat cu probleme in care cea de-a doua valoare numerica se raporteaza la prima (lucru cunoscut la elevi), iar cea de-a treia fie cea de-a doua , fie la prima si doua luate la un loc.
Exemplu :
'La o florarie au venit spre vanzare 250 de garoafe rosii, cu 25 mai multe garoafe albe si garoafe roze cu 25 mai multe decat albe. Cate garoafe roze au venit spre vanzare?
Dupa rezolvarea problemei am solicitat elevilor sa se gandeasca la alta intrebare pe care am putea-o folosi la problema, stind ca spre vanzare au venit mai multe feluri de garoafe.
S-a facut o noua examinare a problemei, s-a completat schema si rezolvarea astfel
?
? ?
![]()
250g.r.+25 g.a. 25g. roze?
250 + 25 = 275 nr. garoafelor albe
nr. garoafelor roze
250 + 275 + 300 = 825 nr.garoafelor
Formula numerica:
250 + 2 x (250 + 25) + (250 + 25 + 25) = 825
sau (pentru clasa a patra)
250 + 2 x (250 + 25) + 25 = 825
S-a alcatuit si formula literala:
a = nr. garoafe rosii
b = nr. garoafe albe
c = nr. garoafe roze
n = 25
d = nr. total de garoafe
a + (a + n) + (a + n + n) ==> a + b + c=d
Din punct de vedere al rationamentului marea majoritate a elevilor au rezolvat corect.
In cazurile semnalate cu rationamentul gresit si greseli de calcul s-au facut corectarile necesare.
De asemenea in clasa a IlI-a am continuat cu reformularile problemelor, prin folosirea ca necunoscuta a uneia din datele cunoscute ale problemei initiale.
Exemplu:
'La un aprozar s-au vandut intr-o zi 423 kg de cartofi, a doua zi cu 183 kg mai mult, iar a treia zi cat in primele doua zile. Cate kg de cartofi s-au vandut in a treia zi?Cate kg de cartofi s-au vandut in total ?'
423 kg + 183 kg I + II ? kg
Izi a II-a zi a III-a zi
kg de cartofi vanduti a II-a zi
423 + 606 = 1029 kg de cartofi vanduti a III-a zi
423 4+ 606 + 1029 = 2058 kg de cartofi vanduti in total
Reprezentarea figurativa a problemei:
I 423
II __________ ______ ____ cu 183 mai mult
1029
Dupa rezolvare s-a obtinut rezultatul 2058.
Apoi s-a modificat conditia problemei, iar rezultatul folosit in enunt ca data cunoscuta.
Exemplu :
'La un aprozar s-au vandut 2058 kg de cartofi, din care 423 kg in prima zi, cu 183 mai mult in a doua zi, iar restul in a treia zi.'
In continuare s-au formulat si alte enunturi in care au fost trecute ca necunoscute celelalte date ale problemei.
Elevii au lucrat cu placere folosind acest procedeu, capatand incredere in ei.
S-a trecut apoi la rezolvarea problemelor de aflare a doua valori numerice cand se cunosc suma si diferenta lor, deoarece elevii stiau aflarea unei marimi cand se cunoaste una din si "cu cat' sau 'de cate ori era mai mare' sau 'mai mica'.
Exemplu :
'Doi frati au economisit intr-o saptamana 8000 lei. Cati lei a economisit fiecare daca unul a economisit cu 1600 lei mai mult decat celalalt?"
Pentru rezolvare s-a folosit metoda figurativa

I II
9600 : 2 - 4800 (al II-lea)
4800 - 1600 = 3200 (I copil)
6400 : 2 = 3200 (I copil)
3200 + 1600 = 4800 ( al II-lea)
Dupa rezolvarea mai multor probleme de acest gen elevii au constatat principalul lucru in rezolvarea acestora este ipoteza ca ambele valori sunt egale. Am realizat cu elevii si formulele literale ;
(a + b - n): 2 - n = a
(a + b - n) : 2 + n = b
Incepand cu clasa a IV-a am consolidat intregul sistem de lucru: rezolva problemelor prin mai multe procedee, extragerea formulei numerice, elaborarea formulei literale, compunerea de probleme.
Accent deosebit am pus si pe probleme cu continut geometric si pe probleme tipice.
In cazul problemelor cu mai multe operatii schema devine mai complexa si mai mobila in raport cu gradul de dificultate al problemelor.
Ca rezultat al unei invatari active, schema usureaza procesul de rezolvare a unor probleme prin folosirea calculelor neefectuate anterior sub forma de exercitii combinate. Pentru a ilustra ceea ce am relatat sa luam exemplu problema:
In trei depozite sunt 148340 kg zahar. In primul sunt 78548 kg, iar in al doilea cu 27038 kg mai putin decat in primul. Cate kg sunt in al treilea depozit ?'
Formula numerica este :
Formula literala este :
(a + b + c) - (a + (a - n)) = c
aceasta deoarece schema problemei este :
a+b+c_____________a________________?b_________________?c
148340 78548 a-27038 (a+b+c)-(a+b)
Planul de rezolvare al problemei:
Zaharul din al doilea depozit
78548-27038 = 51510 kg
Zaharul din cele doua depozite
78548 + 51510- 130058 kg
Zaharul din al treilea depozit
148340- 130058 = 18282 kg
Dupa ce si-au insusit modul de utilizare a schemei, elevii au avut posibilitate libertatea in alegerea ei, fapt ce a dus la o diferentiere in activitatea de munca independenta.
Sa luam o problema pentru a exemplifica acest lucru:
'Intr-un hambar simt 23241 de grau, secara de 3 ori mai putin decat grau, porumb de 4 ori mai mult decat secara, iar orz cu 680 t mai putin ca porumb. Cate t de orz sunt in magazie?'
Problema este scrisa pe tabla.
Elevii au primit numai fisele cu cerintele.
Se insuseste textul, se explica eventualele lucruri neintelese, apoi se trec la rezolvare.
Grupa I avansati Grapa II mediocri
1. Rezolvati problema prin exercitiu, 1. Rezolvati problema cu plan facand la alegere
facand schema invatata. si schema.
2. Scrieti o alta intrebare problemei si 2. Scrieti formula numerica de rezolvare.
rezolvati-o !
Grupa a IlI-a ramasi in urma la invatatura
Urmareste schema si rezolva problema cu plan .
a_________________?b_____ _______ ______ _______? c __________________?d
a:3 bx4 c-680
Grupa a IV-a cu capacitate scazuta la invatatura
a ? b ? c ? d
2324 a:3 bx4 c-680
1. secara 2. porumb 3. orz
Astfel, lectia capata prin modul de rezolvare, ilustrat cu problemele de mai sus, o noua orientare, ample si noi valente formative.
Schema, ca metoda de lucru, pe langa faptul ca sporeste caracterul aplicativ algoritmilor matematicii, ne da posibilitatea sa cunoastem permanent gradul de functionalitate al gandirii elevilor, precum si ritmul de munca al acestora, ca in functie de aceasta cunoastere sa putem asigura sprijinul la timp si adecvat elevilor care intimpina dificultati in munca, folosind activitatea diferentiata in scopul recuperarii golurilor din cunostintele elevilor.
|
Politica de confidentialitate |
| Copyright ©
2025 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |