Utilitatea
In literatura de specialitate notiunea de utilitate a fost introdusa in ideea precizarii clare a proprietatilor pe care trebuie sa le indeplineasca o functie de eficienta.
Se cunosc doua posibilitati de introducere a conceptului de utilitate: utilitate ordinala (introdusa in baza unui sistem axiomatic) si utilitatea cardinala (introdusa in baza unor conditii impuse de practica unor reguli de piata).
1.1.1. Utilitatea ordinala
Se
porneste de la o multime de entitati E numita multimea rezultatelor, pe care se introduce o
relatie binara numita relatie de preferinta;
daca ![]()
![]() atunci rezultatul x este preferatul lui y.
atunci rezultatul x este preferatul lui y.
Se
introduce, de asemenea notiunea de experiment prin notatia ![]()
![]() , unde: p
reprezinta ponderea rezultatului x;
1−p reprezinta ponderea rezultatului y.
, unde: p
reprezinta ponderea rezultatului x;
1−p reprezinta ponderea rezultatului y.
Este
evident ca daca ne raportam la rezultatele x1,x2, ., xn IE, experimentul asociat se noteaza ![]() , unde p1, p2,
., pn reprezinta ponderile acestor rezultate.
, unde p1, p2,
., pn reprezinta ponderile acestor rezultate.
Utilitatea
se introduce sub forma unei functii ![]() care indeplineste
conditiile urmatoare (ne vom raporta doar la doua rezultate
oarecare x, y, precum si la
experimentul generat de acestea):
care indeplineste
conditiile urmatoare (ne vom raporta doar la doua rezultate
oarecare x, y, precum si la
experimentul generat de acestea):
1.
daca ![]() ;
;
2.
![]()
Altfel spus utilitatea este o functie monoton crescatoare in raport cu preferinta, iar utilitatea unui experiment este egala cu valoarea medie a utilitatilor rezultatelor care compun experimentul.
Observatia
1.1. Daca
ne situam in cazul experimental ![]() atunci utilitatea lui
este data de egalitatea urmatoare:
atunci utilitatea lui
este data de egalitatea urmatoare:
![]()
Axiome de comportament rational
Este o problema importanta in practica financiara a carei rezultate are la baza notiunea de utilitate ordinala. Primul sistem de axiome din punct de vedere comportamental a fost introdus de Neumann in 1935 si imbunatatit ulterior de Savage, Luce si Raiffa.
Considerand
experimentul ![]() axiomele de
rationalitate ale lui Luce-Raiffa sunt urmatoarele:
axiomele de
rationalitate ale lui Luce-Raiffa sunt urmatoarele:
1. tabilirea ordinii rezultatelor posibile
pentru orice xi
si xj avem ![]() sau
sau ![]() (orice rezultate sunt
compatibile);
(orice rezultate sunt
compatibile);
are proprietatea de tranzitivitate, adica: ![]() .
.
In baza acestor ipoteze se introduce notiunea de experiment compus.
Vom
presupune in continuare ca ![]() si vom nota prin A experimentul
si vom nota prin A experimentul ![]() , iar prin A1,
A2, ., An experimente ce au ca rezultate x1, x2, ., xn.
Atunci experimentul
, iar prin A1,
A2, ., An experimente ce au ca rezultate x1, x2, ., xn.
Atunci experimentul ![]() se numeste experiment compus.
se numeste experiment compus.
2. Reducerea experimentelor compuse (la experimente simple)
Un experiment compus este echivalent cu un singur experiment simplu
![]()
unde: ![]() ,
, ![]() fiind probabilitatea
entitatii xj in
experimentul simplu Ei,
fiind probabilitatea
entitatii xj in
experimentul simplu Ei,
![]() ;
; ![]() .
.
3. Continuitatea
Pentru
fiecare rezultat xi
exista un numar real ![]() astfel incat
astfel incat ![]() ceea ce se mai poate
scrie
ceea ce se mai poate
scrie ![]() . Deci orice rezultat este echivalent cu un experiment
determinat de primul si ultimul rezultat.
. Deci orice rezultat este echivalent cu un experiment
determinat de primul si ultimul rezultat.
4. Echivalenta
![]()
5. Tranzitivitatea
Preferinta si echivalenta sunt tranzitive. Prin urmare avem urmatoarele relatii:
![]()
6. Monotonia
![]()
In baza acestor axiome notiunea de functie de utilitate introdusa anterior poate fi nuantata prin precizarea proprietatii de liniaritate.
Definitia 1.1. Functia de utilitate
![]()
este liniara daca
oricare ar fi experimentele simple A1
si A2 si ![]() .
.
Pornind
de la aceasta definitie se poate arata ca o proprietate
importanta a functiei de utilitate este aceea ca este unica
pana la o transformare liniara pozitiva. Altfel spus, daca u1 si u2 sunt functii de
utilitate, vor exista constantele reale si pozitive a, b astfel incat ![]()
1.1.2. Utilitatea cardinala
Este un concept important utilizat in teoria deciziilor si mai apropiat de rezolvarea unor probleme de factura economica. Fundamentele teoriei cardinale ale utilitatii au fost formulate de L. Warles (unul din creatorii scolii matematicii in economie).
Functia
de utilitate se noteaza cu u, ![]() , cu precizarea ca
, cu precizarea ca ![]() reprezinta
cuantificarea gradului de satisfacere a consumului bunului
reprezinta
cuantificarea gradului de satisfacere a consumului bunului ![]() .
.
Prin
notatia ![]() se intelege
gradul de satisfacere realizat de componenta x1 a bunului x
(ale carui componente sunt bunurile partiale x1, x2, ., xn).
se intelege
gradul de satisfacere realizat de componenta x1 a bunului x
(ale carui componente sunt bunurile partiale x1, x2, ., xn).
La baza introducerii conceptului de utilitate cardinala sta un sistem de ipoteze, cele mai importante fiind urmatoarele: raportarea constienta intre un bun si o nevoie a lui, inexistenta bunului in proprietatea consumatorului, accesul la bun se face prin piata.
Presupunem ca functia de utilitate u este derivabila partial in raport cu fiecare componenta.
In
acest caz vectorul ![]() este gradientul functiei de utilitate si
semnifica din punct de vedere economic un vector ale carui componente
sunt utilitatile marginale in raport cu bunurile consumate.
este gradientul functiei de utilitate si
semnifica din punct de vedere economic un vector ale carui componente
sunt utilitatile marginale in raport cu bunurile consumate.
Proprietatile care trebuie indeplinite de catre functia de utilitate u sunt urmatoarele:
1) ![]() (daca nu se realizeaza un consum
utilitatea este nula);
(daca nu se realizeaza un consum
utilitatea este nula);
2) ![]() (utilitatea
creste o data cu cantitatea de bunuri consumata);
(utilitatea
creste o data cu cantitatea de bunuri consumata);
3) ![]() (daca consumul
este foarte mic, deci nevoia este practic neacoperita, atunci gradul de
satisfactie este foarte mare in cazul consumului unui bun greu de
procurat. Altfel spus, utilitatea marginala in raport cu un bun oarecare
este foarte mare atunci cand nevoia de bunuri este neacoperita);
(daca consumul
este foarte mic, deci nevoia este practic neacoperita, atunci gradul de
satisfactie este foarte mare in cazul consumului unui bun greu de
procurat. Altfel spus, utilitatea marginala in raport cu un bun oarecare
este foarte mare atunci cand nevoia de bunuri este neacoperita);
4) ![]() (gradul de
satisfactie nu mai creste atunci cand consumul este foarte mare);
(gradul de
satisfactie nu mai creste atunci cand consumul este foarte mare);
5) ![]() , adica
, adica ![]() (aceasta inseamna
ca utilitatea marginala este descrecatoare).
(aceasta inseamna
ca utilitatea marginala este descrecatoare).
Daca se noteaza cu um utilitatea marginala, atunci in cazul in care bunul are o singura componenta notata uzual Q reprezentarile grafice ale utilitatilor cardinale si utilitatii marginale sunt date in figura 2.1.
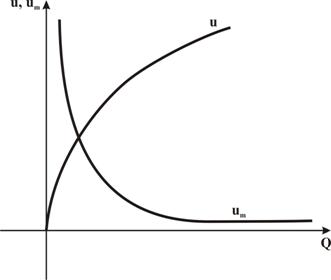
Figura 2.1.
Exemplu Sa se verifice
daca ![]() , indeplineste cerintele pentru a fi functie
de utilitate.
, indeplineste cerintele pentru a fi functie
de utilitate.
Rezolvare: Pentru ca ![]() sa fie
functie utilitate trebuie sa satisfaca urmatoarele
conditii:
sa fie
functie utilitate trebuie sa satisfaca urmatoarele
conditii:
1.
![]() ;
;
2. 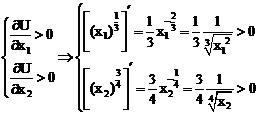 ;
;
3.
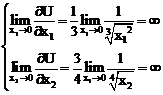 ;
;
4.
 ;
;
5.
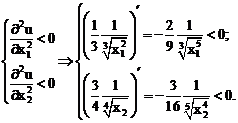
In
concluzie ![]() este functie
utilitate.
este functie
utilitate.
|
Politica de confidentialitate |
| Copyright ©
2026 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |